Mapping to lower case

In the last lesson, we asked you to implement this function:

The first thing it should do is apply the palindrome-testing function, and we want to do that inside a case expression so that we can then pattern match over the three possible results.

nonemptyPal might return one of three things:

• Nothing (invalid input)
• Just False (not a palindrome)
• Just True (yes, a palindrome)

You have written case expressions before, but one thing is different here: we have a function application inside the case expression – what we’re pattern matching over isn’t merely word, but nonemptyPal word – we’re matching over the cases of the result after we apply nonemptyPal to the word value.

For each of the three possibilities, on the right side of the -> arrow we write our message.

And that’s our verbose function. We can now also update main to make the program friendlier.

Try it out:

λ> main

"Please enter a word."

Now when we enter an empty string, we get “please enter a word”, which is probably more helpful for our user than “nothing”.

Next we want to address the problem that our program doesn’t accept a palindrome if it’s capitalized.

λ> main
Mom
"Sorry, this is not a palindrome."

λ> main
mom
"Yay, it's a palindrome!"

If we write “Mom” with the first M in upper case, we think that ought to count as a palindrome, so let’s update our code to make that happen.

Here’s one approach we could take: suppose we had a way to convert the entire input to either upper or lower case. We’ll go with lower case. If we have a string that has some mixture of upper and lower case letters, we’re going to convert them all to lower case, so we’ll convert Mom to mom. Then it will be more readily recognizable as a palindrome.

The standard library doesn’t give us exactly this function, but we can write one. We’ll call it all lower case. Its input is String, and its output is also String – the type of the value doesn’t change as it undergoes this case modification.

That’s just the type signature, for now, and we’ll write that function in just a minute. But first, we can think ahead to what this function is for. Once we have that function, here’s how we’ll use it:

We apply allLowerCase to the word first, and once everything is lower-cased, then we apply the isPalindrome function. Converting the whole input to lower case obliterates all distinctions between upper and lower case letters, and so capitalization should no longer have any way to effect whether something is considered a palindrome or not.

So now we have to go back and actually write this allLowerCase function.

A word is a list of characters, so what we’ll need to do is change each character to lower case one-by-one. So we’ll put off writing allLowerCase a little longer, and first write a smaller function that just words with a single character.

Recalling our spell function, we could write a case expression and start enumerating each input, and its corresponding output:

We’re not actually going to write all this out! Fortunately, the standard library already comes with a toLower function.API documentation for toLower It isn’t a part of the Prelude module, because the powers that be have not deemed this to be a function so obviously important that everyone writing a program will nearly always want it. But it is there, just tucked away in another module.

We haven’t really talked about what modules are - a module is a collection of types and functions that somebody has written for you to use. There are around a hundred general-purpose modules that come with the compiler, and way more that people have written in libraries that you can download.

Fortunately, Haskell has a really good search engine to help find things if you don’t know what module they’re in. It’s called “Hoogle” (because it’s sort of like the “Google” for Haskell). It is a really great tool, and both beginning and experienced Haskellers use it all the time.

We’ve mentioned that the function we’re looking for is called toLower, so we can type that in:

It gives results as you type. A lot of stuff comes up here, because there are a lot of modules that define different functions with this name. Notice that a lot of the results have different types than the one we’re looking for – there toLower functions with types like Text -> Text, or Word8 -> Word8, etc. One thing we can do to narrow it down is type the entire type signature into the search box: “toLower :: Char -> Char”.

And in this case we can narrow it down even further by specifying that we only want to search for things that come with GHC, not just any code that anybody’s ever published. From the select box, choose “set: included-with-ghc”.

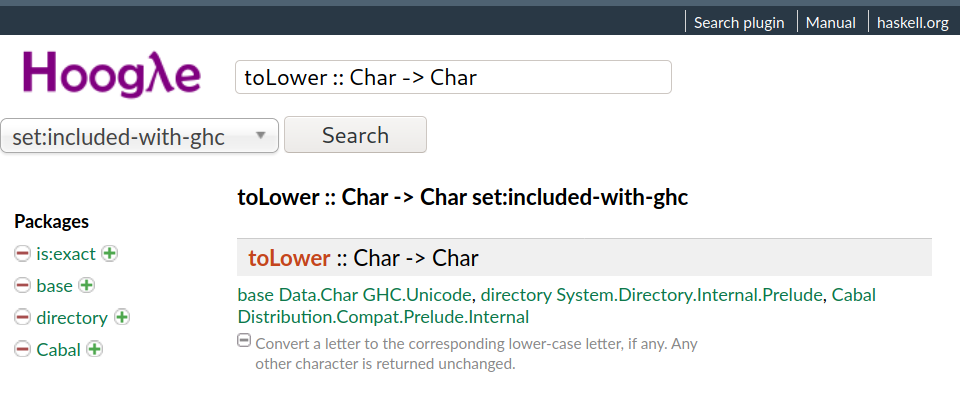
So that gets us down to a single result. We could click on that to go to the full documentation page, but all the information we need is right here – The module name we’re looking for is called Data.Char, which contains a lot of functions related to characters – and the description of what this function does is written underneath:

Convert a letter to the corresponding lower-case letter, if any. Any other character is returned unchanged.

So, the point of all this is: Back in our source file, we need to import that module to announce that we intend to use its stuff. Adding this line to the file means that when we load the file into GHCi, the functions that we’re using from this module will be available as GHCi interprets our file.

This import statement brings the entire contents of the Data.Char module into scope. Since our palindrome program deals heavily with strings, perhaps there are other things in this module that we will end up wanting to use.

So now let’s get rid of our toLower function, because we can use the one that we’ve imported. We’re back to trying to write this allLowerCase function.

Given that we have a function that can lower-case a single character, how do we turn that into a function that can lower-case an entire list of characters?

If you know another programming language, you may already know this function - It goes by the name map in Python, Clojure, Java, Scala, JavaScript. In Haskell, we call it map, and it is available in Prelude. We’re going to implement our own map function, because it’s a really good exercise, and a great opportunity to try out pattern matching on lists.

We’ll call it “my map” just to give it a different name from the Prelude function that’s already there.

We will be using toLower as the argument for that (a -> a) parameter. In that case, a will take on the type Char, and [a] will be a list of characters (in other words, String).

Let’s take a moment to contemplate this type. There are two ways to think about it, and both are really valuable and equally true.

You can think of myMap a function with two parameters.

1. This (a -> a) transformation
2. The input list

And it returns an output in which the transformation function has been applied to each element of the input list.

You can also think of myMap as a way to convert a transformer of single a values into a transformer of lists of a values.

These are the exact same thing, they’re just two different ways to think about it.

For right now, to implement this function, we’re going to think about it in the first way. A function with two parameters:

Now we have to start pulling the list apart to get at the individual elements inside. The main tool we have for reckoning with what’s inside of something is the case expression.

Every time we write the word case, we should be thinking about what the constructors are. Remember a list has two constructors, so most of the time we pattern match over a list, we’ll want two cases: the empty list, and the non-empty list. We have already seen what pattern matching on the empty list constructor looks like:

But the last time we did this, we didn’t really think about the nonempty list constructor; we just used the underscore to catch them. This time we need to think through what a “nonempty list constructor” looks like.

So, let’s remind ourselves of the list type definition:

One constructor is that empty list that we’ve already seen. The other constructor is a value appended to a list of more of those values. In Haskell, we most often deconstruct values in the same way that we construct them.

We want to take a moment to show you something about strings. We’ve been writing strings like this:

λ> "julie"
"julie"

And that’s very convenient. But it’s a shorthand notation. Watch.

λ> 'j' : "ulie"
"julie"

We can use that cons constructor from list to make lists, and in fact, below the surface, that’s how lists are both constructed and deconstructed. The shorthand notation of putting all the elements into brackets or quotation marks without any cons operators is convenient, but you have to look beneath the surface to break lists apart, element by element.

λ> 'j' : 'u' : "lie"
"julie"

λ> 'j' : 'u' : 'l' : 'i' : 'e' : []
"julie"

So we know that for our eventual map function we need to be able to apply a function that takes a single character as input to each element, successively, in a list. So we’re going to need to make use of this knowledge of how to break lists into elements, step by step, in order to break the input list into elements we can process one by one.

There’s a standard library function that takes a list as input and just returns the first element of that list, assuming the list isn’t empty.

λ> :type head
head :: [a] -> a

λ> head "julie"
'j'

The head function is doing some deconstruction of the input list – it’s breaking the list up into two pieces, the first item and the remainder, and just giving you the first item.

There’s a corresponding function called tail that returns everything except the first element.

λ> :type tail
tail :: [a] -> [a]

λ> tail "julie"
"ulie"

With list deconstruction, these are fairly straightforward to write yourself.

Notice how we break the list parameter apart into elements we’ve called first and rest (for, “the rest of the list”) separated by the cons operator. We don’t need to do anything more to break it apart except write the parameter this way.

Now there is not a good way to write head with the same type as it has in the standard library, and adequately handle the empty list. You have to return an a, not a list – and if the input is [], there is nothing that we could return.

Since tail returns a list, though, we could make it have a case that matches the empty list and returns the empty list, and also a case that is just like the myHead function except that it returns the “rest” of the list, minus the element we called first.Note that this is not the same as the Prelude tail function, which is undefined for the [] input.

We can try it out:

λ> myHead "julie"
'j'

λ> myTail "julie"
"ulie"

So as we can see above, cons is the constructor we need to pattern match on for nonempty lists. That was quite a digression, but now we can go back to our map function. Now we know what the second constructor in our case expression looks like.

Cool. Now we just need to figure out what we want each of these cases to map to! For that, we need to talk a little bit about recursion.

Recursion is the process of a function applying itself, which can sound weird at first. What this means is that we want to break a function like this down into three parts:

1. Do something to the first element of the list.
2. Then do it again and again, pulling one element off the head of the list at each step, so the rest list is getting smaller and smaller.
3. Stop when we hit the empty list because there are no more elements to apply a function to. The empty list is, as we see, always trailing along behind the elements of the list, under the surface. This third step (which will go first in our case statement) is often called our “base case” or our stopping condition.

This is conceptually how the lower-casing the string “JULIE” will proceed:The ++ operator here is concatenation, the joining of two lists together.

To evaluate map toLower "JULIE", the map toLower function is actually applied six times. The argument gets progressively smaller with each application.

We’ll show one more example like this, but with numbers instead of characters this time. Remember, all of these forms are equivalent:

• [1, 2, 3] – The special bracket list notation
• 1 : (2 : (3 : [])) – Explicitly showing all of the constructors
• 1 : 2 : 3 : [] – Same as previous, but without the parentheses
• 1 : [2, 3] – A mixture of cons and the bracket notation

We switch between these forms below to illustrate how the list [1, 2, 3] is broken down and reconstructed when we use map to multiply each number by ten, yielding [10, 20, 30].

So, this is what we’re talking about when we talk about map being a function that applies itself. Each time, the list parameter gets smaller, the item that’s the head of the list changes, until we finally apply it to the empty list, which provides our stopping condition.

The three things we need to think about:

1. Do something to the first element of the list;
2. Apply the function to the remainder of the list to keep doing that again and again;
3. Think about what the stopping condition will be. In this case, when we have any empty list, there are no more items to do anything to.

So, let’s get back to writing our function. The stopping condition is covered by the [] -> case: when we get the empty list constructor, we return the empty list.

To do something to the first element of the list, we apply func to that first list item.

We have to have a cons operator so we can rebuild the list, and then this is where the recursive part comes in. We will create this process of pulling one element off the “rest” of the list by calling this function again. We use this same myMap function to keep doing the same thing over and over, pull one element off the list, apply func to it, and then go on to the rest until there’s nothing left.

Reload and try the multiplication-by-ten example:

λ> :reload

λ> myMap (* 10) [1, 2, 3]
[10,20,30]

At long last, we can go back to our allLowerCase function and complete it. It will take a String that might have uppercase characters in it and transform it into a String that is entirely lowercase.

Let us again reload and try that out.

λ> :reload

λ> allLowerCase "JULIE"
"julie"

We can actually write this function without the word parameter.

This allLower function still works the same as allLowerCase, even though we took out the parameter! The type of allLower still has a String parameter, but it isn’t included in our definition. How does this still make sense?

Here is where you might want that second way of thinking about the type of myMap that we mentioned earlier.

We can think of it as a function of one parameter – the function to apply to each item – and its result type is this [a] -> [a] function. If we apply myMap to toLower, the result we get is a String -> String function. And that’s what we want!

We’re not going to dwell on this here, but this notion that every function really just has exactly one parameter has a lot of nice ramifications in Haskell.

Inspect the type of the map function that comes from Prelude:

λ> :type map
map :: (a -> b) -> [a] -> [b]

What is the difference between the type of the myMap function that we wrote and the type of the standard map function? Could we use map instead of myMap in the definition of allLowerCase?