Understanding contravariance

The Functor typeclass provides one basic way to lift, but lifting doesn’t stop there; several other typeclasses provide lifting operations. Applicative, Monad, and Bifunctor can be viewed as fmap with a little something extra. These functors all have lawful implementations of fmap, but not all functors have lawful implementations of the lifting operations from these other classes. There are more functors than there are applicatives; more applicatives than there are monads.

Contravariant and Profunctor, though, are quite different. We’ll just be talking about Contravariant here. After this, you may wish to go on to Bifunctor and Profunctor. Very many functors are covariant functors, while relatively few functors are contravariant.

When you start exploring contravariant functors, you may at first think the type of the primary method, contramap, is contraintuitive:

Compared to fmap, this seems strange – how do we pass an a0 to our a0 -> a1 function when what we have is an f a1? How can we transform an a0 -> a1 into an f a1 -> f a0? Somehow a result type will need to be adapted into an input type.

The first thing to do in trying to understand Contravariant Data.Functor.Contravariant is to understand what sorts of type constructors are contravariant. Let’s ask the REPL using the :info command: Some output from GHCi has been elided here for brevity.

λ> import Data.Functor.Contravariant

λ> :info Contravariant
class Contravariant (f :: * -> *) where
  contramap :: (a0 -> a1) -> f a1 -> f a0
instance Contravariant Predicate
instance Contravariant (Op z)
instance Contravariant Equivalence
instance Contravariant Comparison

λ> :info Predicate
newtype Predicate a = Predicate {getPredicate :: a -> Bool}

λ> :info Op
newtype Op z a = Op {getOp :: a -> z}

λ> :info Equivalence
newtype Equivalence a
  = Equivalence {getEquivalence :: a -> a -> Bool}

λ> :info Comparison
newtype Comparison a
  = Comparison {getComparison :: a -> a -> Ordering}

Notice what these types all share: They are all wrappers around functions. That narrows the field of what we need to understand considerably!

That’s especially interesting because there is also a covariant functor related to functions; that is, there is a lawful Functor instance based on the type constructor (->). Let’s back up for a moment and see what the covariant functor can teach us.

When you first learn about the Functor class with its definition of fmap, you may have thought of those f types as “containers” For an argument that functors really are containers, see Functors are Containers by Bartosz Milewski. or “wrappers” For a more lighthearted take, try Monads are like burritos by Mark Dominus. and learned to understand them first as things like Maybe and lists. That understanding works fine until you find out about the functor of functions, when suddenly the f is (a ->) and the world shifts just a bit.

Typically when learning Haskell, people learn about function composition before they learn about the Functor typeclass, or perhaps they’ve learned about composition from a math class prior to ever learning Haskell. At any rate, it is often a surprise for people to learn that function composition is the fmap of functions, or, more precisely for the type constructor ((->) a). Let’s take a moment to understand why this is so.

As we said above, functors lift a function z0 -> z1 to a function f z0 -> f z1 where f is some type constructor. The type constructor for functions looks like this (simplified a bit):

It’s a special datatype, and yet for the purposes of talking about the Functor instance, it works similarly to a pair or two-tuple type. As usual for type constructors with more than one type parameter, we must partially apply this constructor to write the instance.

Note that (->) a is equivalent to (a ->).

We’ve already said that this implementation of fmap is the same as (.), but we want to prove it to ourselves.

Recall the general type of fmap:

We know the f here will be (->) a, so f z0 is ((->) a) z0 and f z1 is ((->) a) z1. Thus our fmap specialized to (->) a looks like this: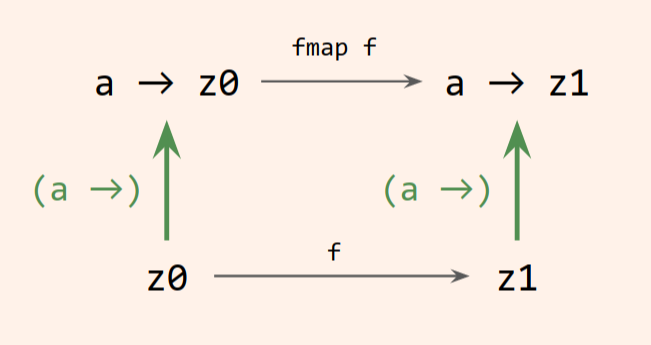

We can rewrite that with the arrows in infix notation as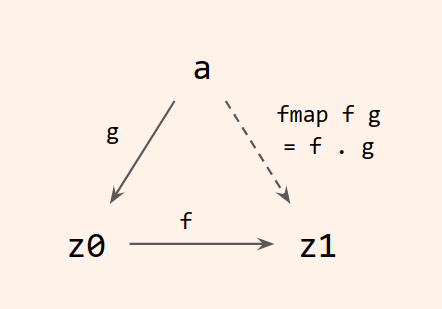

Let’s compare that directly to the type of function composition:Data.Function

If we label the (->) a type constructor f, then we see how we get directly from the type of composition to the type of fmap.

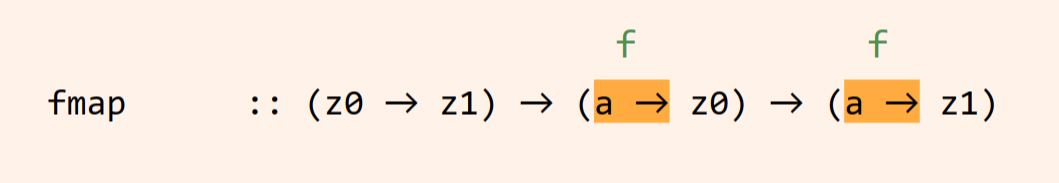
Thus we can finish our fmap implementation by defining it as function composition.

We can think of this as lifting a function into a context of another function. Lifting a function into a function context provides a context in which it can accept as input the output of another function. If we have a function f :: a -> z0 but we need a function a -> z1, then a function g :: z0 -> z1 takes us there via fmap g. When we lift g into the context of (a ->) via fmap g, we adapt f from a -> z0 to a -> z1 by post-processing its result.

To put another way: The type constructor (->) a z is covariant in its second argument.

Now it’s time for something completely different.

Contravariant functors reverse the direction of composition. Covariance and contravariance on Wikipedia

This gives us a good place to begin our investigation into contravariance – by writing a reversed function composition.

We want to write a “contra-composition” function that compares to regular (covariant) composition like this:

The implementations also resemble each other.

We can see that the only difference here is that it we have flipped the order of the arguments. And if we experiment with these in the REPL, we would get the expected results:

λ> comp (< 10) length [1..20]
False

λ> contraComp length (< 10) [1..20]
False

This isn’t a super compelling example; why would you particularly want to flip the application order around like this? We’ll ask you to defer judgment on that question until we can get to some more interesting examples in a bit.

But the upshot is:

1. If we have a function a -> z0 and we need a -> z1 then we need to change our result types, so we need an “adaptor” function z0 -> z1 to get there.
2. If we have a function a0 -> z and we need a1 -> z, we have to change the input type. We need a function from a1 -> a0 to get there.

With covariant composition, we wanted to change the result type and did so by passing it to an adaptor function. Now we want to change the input type by pre-processing the input before passing it off to our original function.

Contrasting Functor versus Contravariant, we can see this by annotating the composition types like this:

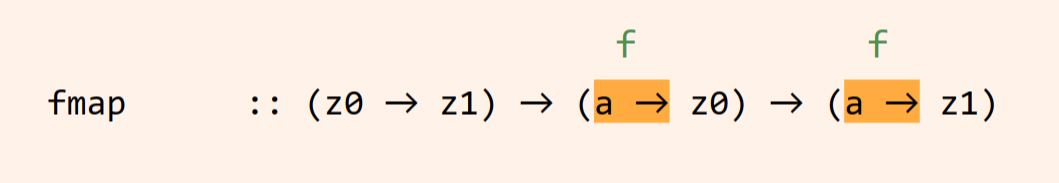
With covariant right-to-left function composition, the f constructor represents fixing the type of the function’s input. With the contravariant, left-to-right functor of functions, the f' constructor represents fixing the type of the function’s result.

By “fixing”, we mean a shorthand for it being a free, or unbound, variable. For example, if we say, “consider Either a b where a is fixed”, we mean “consider \b -> Either a b.” The a is arbitrary, but for the purposes of the discussion it’s not the input variable for the functor – b is the input variable for the functor. So when we say that (->) a b is covariant in its second argument and fixes the type of the input, we’re saying that, whatever the type of a, it isn’t the object of our concern; we’re not going to touch it or transform it or adapt it. It’s a black box as far as our composition is concerned.

What we just did above is a good gateway to understanding the Contravariant class and its contramap method, because contramap is exactly the flipped composition that we just wrote!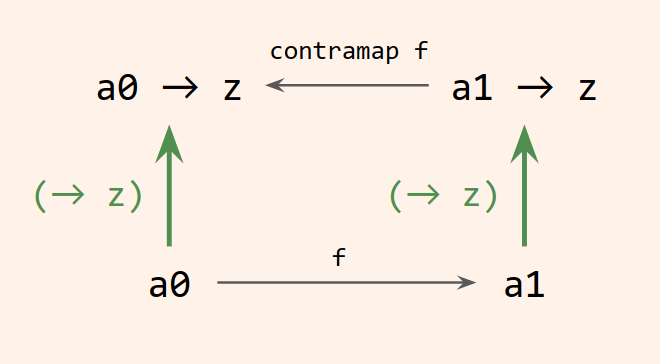

That last instance doesn’t actually compile, unfortunately. We need to wrap the function type in a newtype with the type arguments ordered so that we can fix z and write the Contravariant instance with a as the bound type variable.

We have various choices for newtypes, but the most basic is Op. Op is a wrapper around a function with its arguments flipped:

Let’s talk about this declaration for a moment. Op has two parameters; when we look at the data constructor, we see that the first parameter is the result of a function, and the second parameter is the input. The getOp function allows us to conveniently unwrap an Op value into this underlying function: given an Op z a value as its first argument, it gives us a function a -> z.

Let’s rewrite our contraComp example from above, but using Op.Op

The contramap definition for Op should look familiar, with a bit of extra plumbing:

Compare this to our previous definition of flipped function composition, contraComp:

Or, equivalently:

Let’s see if we can turn our completely contrived length example from above into a fancy contramap example. We want to check lists to see if they are of length 10:

Notice that because Op has its parameters in the reverse order of the wrapped function, the Bool results are the first type argument, while the inputs are the second type argument. isListOfTen takes a list as its input, while isTen takes an Int as input; each returns a Bool.

Remember that contramap length isTen is equivalent to (getOp isTen) . length.

In the REPL:

λ> getOp isListOfTen [1..100]
False

λ> getOp isListOfTen [1..10]
True

What we just wrote using Op Bool is perhaps better captured by the newtype Predicate,Predicate which is a wrapper around a -> Bool functions.

Let’s refactor to use Predicate and its contramap:

Use getPredicate to apply this to a list and run it:

λ> getPredicate isListOfTen [1..100]
False

λ> getPredicate isListOfTen [1..10]
True

Let’s add an additional function to filter a list of lists with our predicate:

Another contravariant functor worth looking at is Equivalence.Equivalence Equivalence is a newtype wrapper around equality relations.

The contravariant package also provides a function called defaultEquivalence that puts == into the Equivalence context, much the way our isTen functions above put (== 10) into the Op or Predicate context.

λ> getEquivalence defaultEquivalence 4 5
False

λ> getEquivalence defaultEquivalence 4 4
True

Now we can use this to check for equivalence on only one side of a tuple by contramapping

If we compare two tuples using a default equivalence, it checks both elements for equality:

λ> getEquivalence defaultEquivalence (1, 2) (1, 3)
False

λ> getEquivalence defaultEquivalence (1, 2) (1, 2)
True

But using the equivalences we wrote above, we can also compare them on just one side or the other:

λ> getEquivalence fstEquivalence (1, 2) (1, 3)
True

λ> getEquivalence sndEquivalence (1, 2) (1, 3)
False

In summary, for covariant functors, the unlifted and lifted functions point in the same direction, z0 -> z1. With contravariance, the unlifted and lifted functions point in opposite directions: one goes a0 -> a1, the other goes a1 -> a0, but reversing the order of composition lets us get where we need to go.

While you can imagine functions like this, that filter some inputs by one or more predicates, all of this could have been written another way. You may have even invented flipped function composition on your own without realizing it had a name! But contravariance really starts to shine in the context of bifunctors. Bifunctors that are contravariant in their first argument and covariant in their second argument are called profunctors.