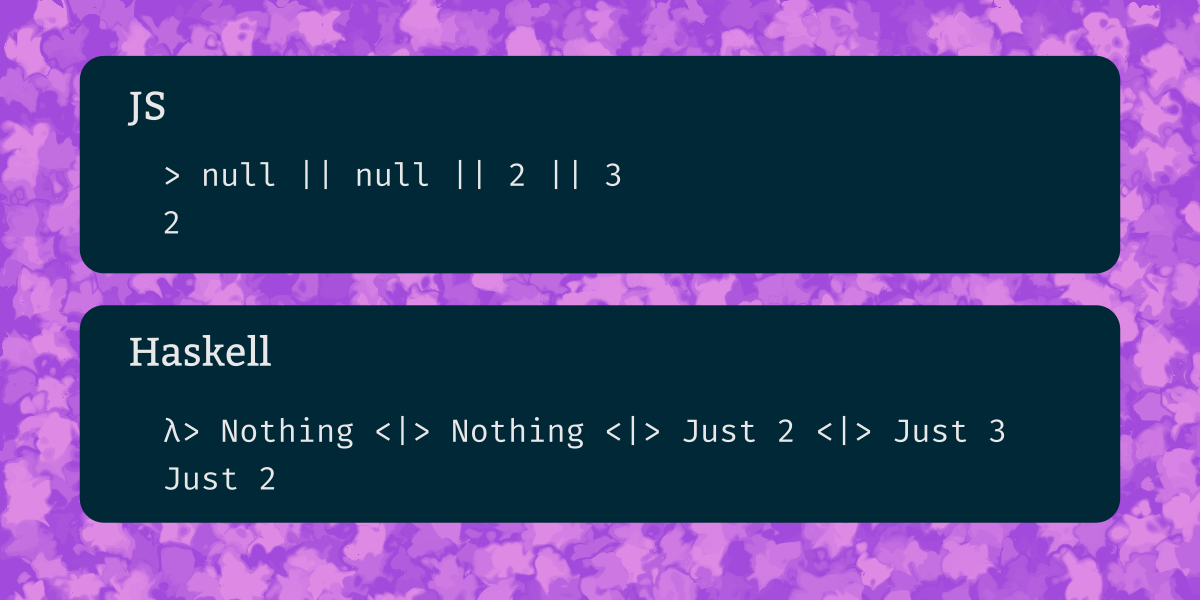
Do you know why Math.min() = Infinity in JavaScript? The answer is about monoids! We compare this odd JavaScript behavior to similar code in Haskell, explore the surprisingly large design space of min/max functions, and talk about why you should care about folds and monoids.

We found a blog post by Greg Heartsfield about generating different fractal sets using Haskell. We were especially attracted to the Julia Set and set about adapting it to our needs.

We used a Mandelbrot set generator written by Cies Breijs to generate some of our header artwork. This article discusses how we used JuicyPixels to colorize it.

Here we give a monitoring server that can aggregate events from multiple processes. This example demonstrates simple inter-process communication using sockets, multi-threaded applications, a daemon that responds to an interrupt signal, and calculating the success-to-failure ratio over a sliding window of event data to assess the health of a service.

The ACME category on Hackage is for joke packages. The name “Acme” is a reference to the name of the company from which Wile E. Coyote obtains dangerous contraptions that always backfire.

The Alternative class is a monoid over applicative functors.

Do-notation has historically been reserved for monadic contexts, most commonly used with IO. The ApplicativeDo extension allows you to use do-notation in an applicative context.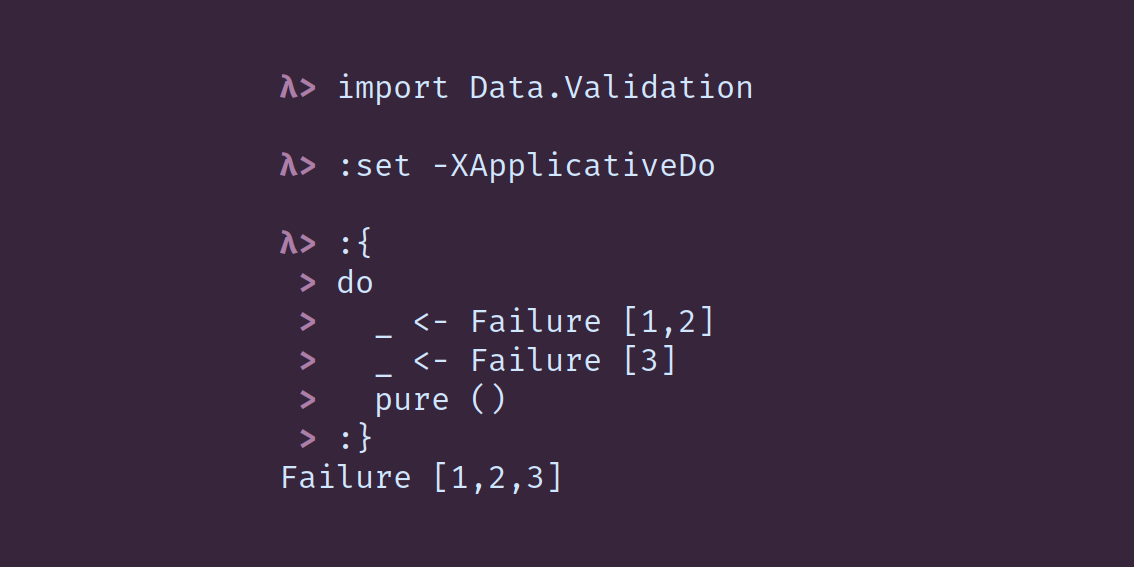

We begin a thorough dive into what the Applicative laws mean and what useful properties they assure. This lesson introduces the algebraic concept of homomorphism and covers two of the four laws: homomorphism and composition.

The Applicative identity and interchange laws are two halves of the a single idea: (pure _ <*>) and (<*> pure _) are both fmap operations that preserve the Applicative structure of whatever value they are applied to. These limitations imposed upon “pure” values assure us that Applicative functors conceal no surprises.

We’re familiar with fmap that lets us lift and apply functions when the values we’re trying to transform are embedded in some other constructor. But what happens if our function is also? That’s what this exciting lesson is about!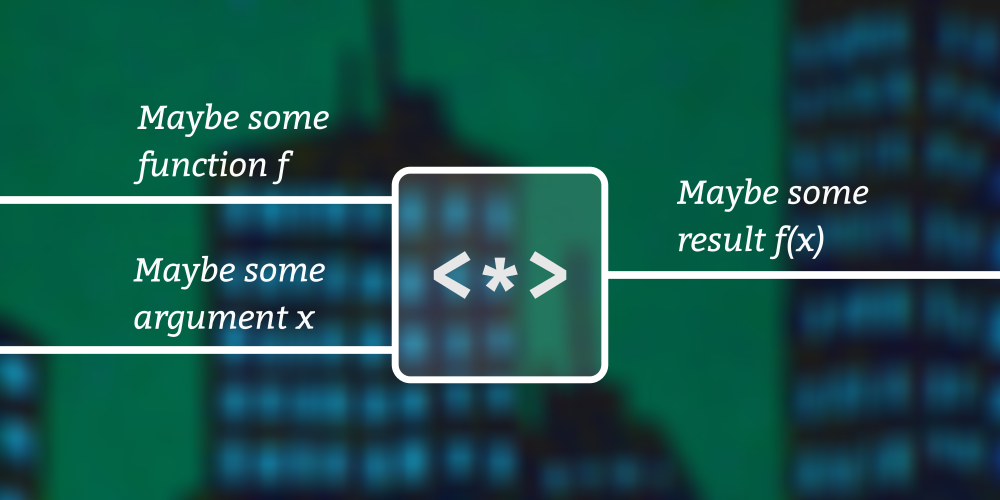

In this lesson, we first take a look at a common applicative idiom, examine the connection between liftA2 and <*>, and then take a careful and thorough look at tuples as applicative functors. What we find under the applicative surface are monoids, oh my!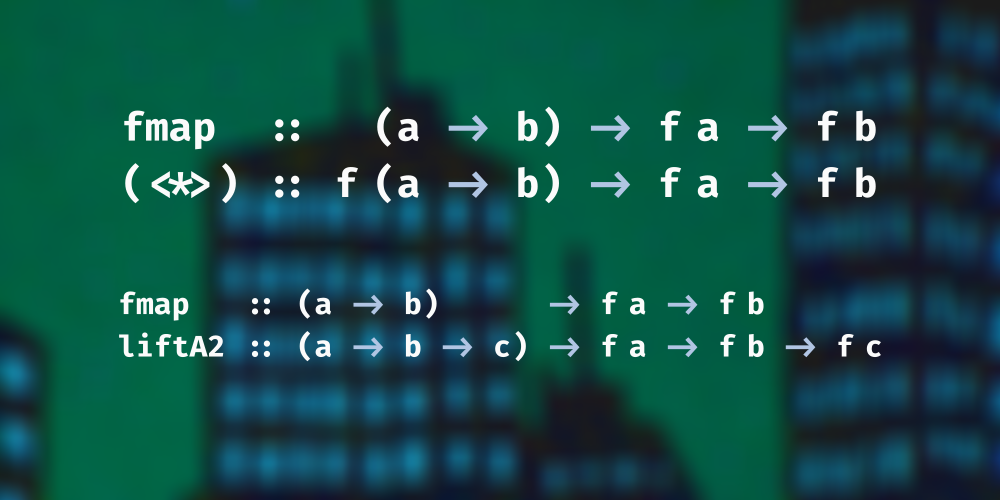

Previously we looked at the connection between <*> and liftA2, their connection to fmap, the pure function, and the monoidal structure of applicatives. We will still want to give some closeup attention to a few other applicatives, especially functions and lists, but this lesson will focus on the other operators in the typeclass (<* and *>) before we move on to those. While you almost never need to implement them yourself – because the compiler can derive them from your implementations of pure and <*> (or pure and liftA2) – they are useful, yet often ignored.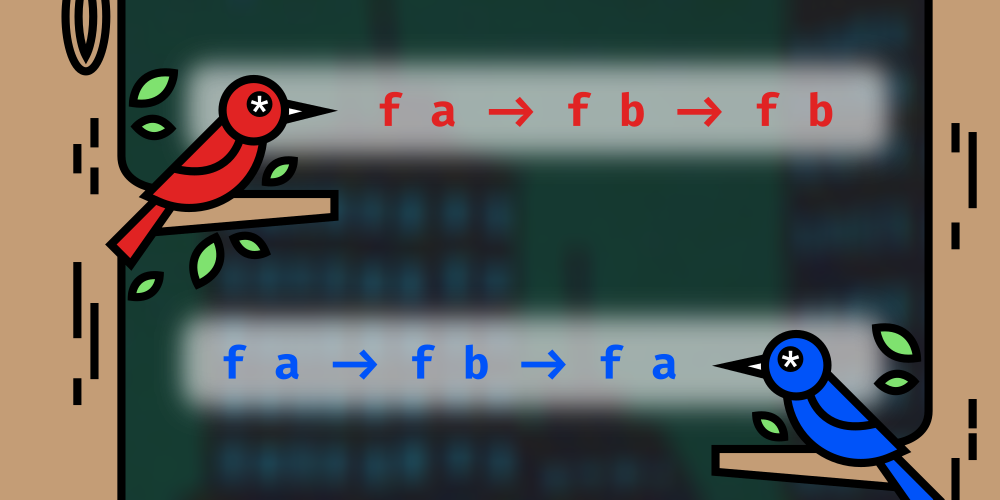

In this lesson we look at lists and spend a little more time with the connection between applicatives and monoids. We do not typically think of types having more than one valid Applicative instance. The connection between a type and a typeclass, expressed in an instance declaration, must be unique. Ideally, there should only one sensible or legal way to implement the functions for that type. And, indeed, that’s how Functor works, which is why we can easily derive Functor instances. And since applicatives are functors, we might expect that to carry over, and most of the time it does work out that way. However, applicatives are not mere functors; they are monoidal functors.

Previously we talked about the Functor for the function type – or, more precisely, for (->) a, the partially applied function type. Looking carefully at the type of fmap instantiated to that type (->) a led us to the revelation that the fmap is identical to ordinary function composition. In this lesson we again discuss the function type, this time looking at its Applicative instance. For the purposes of Applicative, Monad, and monad transformers, we usually refer to it with a newtype wrapper called Reader, so we take our first look at that in this lesson as well.

Previously, we looked at how to combine Reader with IO into one applicative functor that has the flavor of both. This lesson introduces a newtype called Compose that generalizes this idea that any two functors or applicative functors can compose.

We have so far seen with applicative functors that one way to view the Applicative class is that its most notable methods, liftA2 and <*>, are extensions of fmap. So, most functors are also applicative functors. This does not, however, account for pure, which has no companion in the Functor class. In this lesson we’re going to look at why an important data structure called Map is not a valid instance of Applicative. To do that, we’ll consider an alternative to Map alongside Map itself, what their instances would look like, and the problem with pure. This will involve discussion of one of the Applicative laws.

We write property tests for the Applicative laws. The peculiarities of these properties bring up several interesting new Haskell features, including RankNTypes and AllowAmbiguousTypes. The next two lessons make use of the tests we write here.

Most of the datatypes you’re used to follow a simple pattern: the data constructors’ type parameters match up with the kind of the type constructor. This series is about ways to deviate from the regular path and define slightly more exotic types. 1. By placing equality constraints (~) on a data constructor, we can reduce the number of parameters it has relative to the kind of the type constructor; 2. Using the forall keyword in a data constructor, we can increase the number of the type parameters it has relative to the kind of the type constructor. The first lessons will establish some foundations, and subsequent lessons will apply these concepts to practical demonstrations.

If you are absolutely new to Haskell, start with the Beginner crash course. This course is adapted from the six-hour beginner workshop we taught online for ZuriHac 2020. This is not a complete collection of everything you need to know about Haskell; it focuses on a small set of things that new programmers can learn in two days.

The BlockArguments extensions allows certain expressions – most notably do-blocks but also lambda expressions and case expressions – to be used as arguments to functions without use of parentheses or the dollar sign to signal the correct associativity.

Case expressions are useful for conditionals that have two or more branches. Some other languages call this kind of expression a “switch”. Pattern guards can also be used to a similar effect.

The Haskell standard library (a package called base) provides various basic data types. Here we demonstrate only a few of them.

If you replace an expression <expr> with $(lift <expr>), then that expression will be evaluated during compilation. If you have reason to be concerned that evaluation of <expr> may fail, this technique has the benefit of giving you a compilation failure instead of producing a program that fails by throwing an exception at runtime.

The type checker can provide rapid feedback as you code. We recommend using ghcid. It is a small application that runs in your terminal, watches for changes in your source files, and displays any errors that the compiler detects.

Artwork generated using Geoff Hulette’s implementation of Conway’s Game of Life.

The Hashable typeclass is suitable for hash maps, but sometimes we need something a bit stronger. A hash function is a good cryptographic hash if mathematicians are confident that nobody will ever be able to come up with two inputs to the hash function that produce the same output.

Both Haskell98 and Haskell2010 allow datatypes to have contexts, that is, typeclass constraints on the type parameters. Currently this is still allowed only with the -XDatatypeContexts extension turned on, and this feature will be removed from the next Haskell language standard. This article looks at why this feature has been deprecated.

Function declarations in Haskell rely less on parentheses and more on whitespace relative to many other languages.

Most of the code that powers the Type Classes website is written in Haskell and running on Amazon EC2. In this project we walk through the process of how we developed our deploy process. We start by clicking around in the AWS web console, and we end up with some scripts and a fairly simple process that we now use to provision our servers from the command line. We use these command-line tools: nix-build, to compile everything that runs on our sever; nix-copy-closure, to upload build results to the server; ssh, to activate changes on the server and switch to a new build. The scripts we write here are written in Haskell, using: a Stack ‘script’ shebang; the turtle package to run shell commands; the neat-interpolation package with the QuasiQuotes GHC extension.

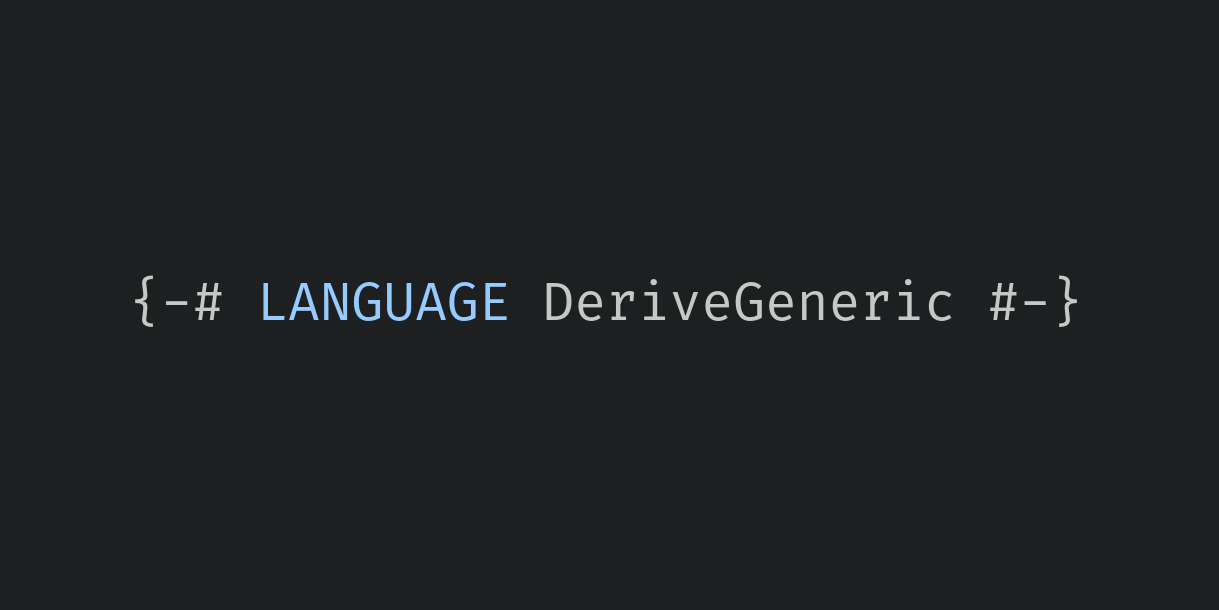
Although it is technically possible to write your own instances of the Generic typeclass, in practice we nearly always let GHC derive it for us. For that, we must enable the DeriveGeneric language extension. Generic can be derived for all but the most exotic datatypes. The DeriveGeneric extension first appeared in GHC version 7.2.1.

The DeriveLift extension allows you to derive instances of the Lift typeclass, which makes it very easy to write expression splices using Template Haskell. In contrast to most derivable typeclasses, the Lift class does not live in base; it comes from the template-haskell package.

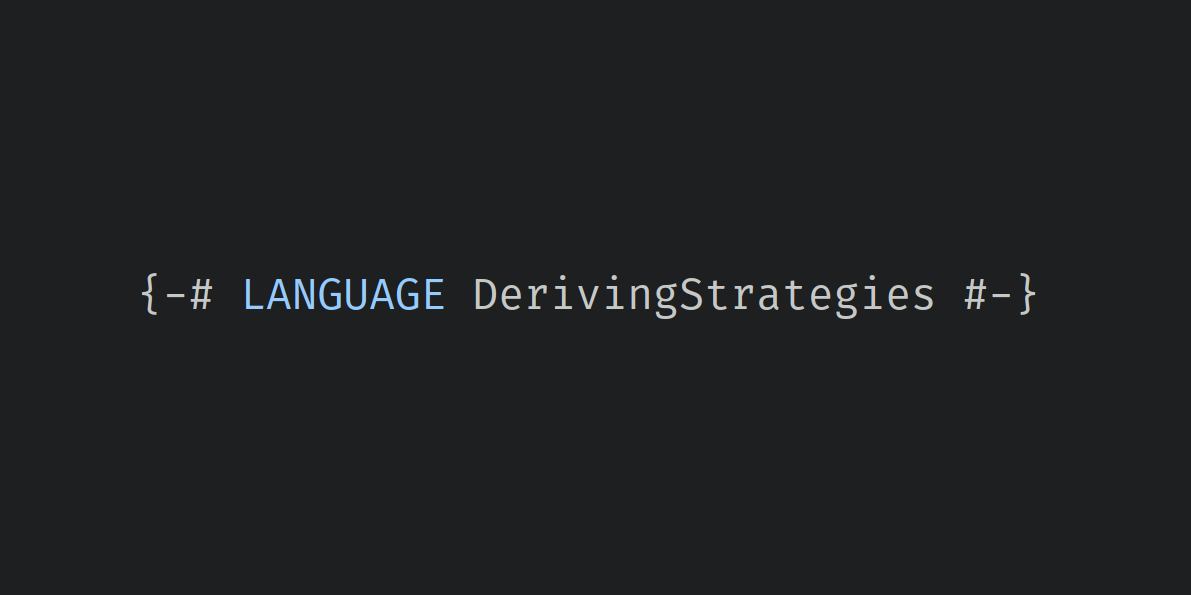
GHC has a number of mechanisms for automatically generating typeclass instances, most of them enabled via language extensions. Some extensions allow the deriving of one particular class; others are more general and can be used with any class. The DerivingStrategies extension, introduced in GHC 8.2, brings them all together into a single more cohesive idea by introducing two syntactic changes: First, a type definition can have multiple ‘deriving’ clauses, not just one. Second, each deriving clause may optionally specify a “deriving strategy” that specifies which deriving mechanism to use for the classes listed in that clause.

The DerivingVia GHC extension provides the ‘via’ deriving strategy, which lets your type copy typeclass instances from other types. The type providing the instances and the type receiving the instances have to be representationally equivalent – more or less the same, distinguished only by one or more layers of newtype definitions.

There are some reasons you might not want the entire contents of the prelude to be implicitly present everywhere: if you are a learner and you want to reimplement parts of base for exercise; if you are an opinionated expert and you dislike many of the things in Prelude; if you are using the RebindableSyntax extension. Here we discuss how to use either NoImplicitPrelude, import statement, or module mixins to remove the prelude from scope.

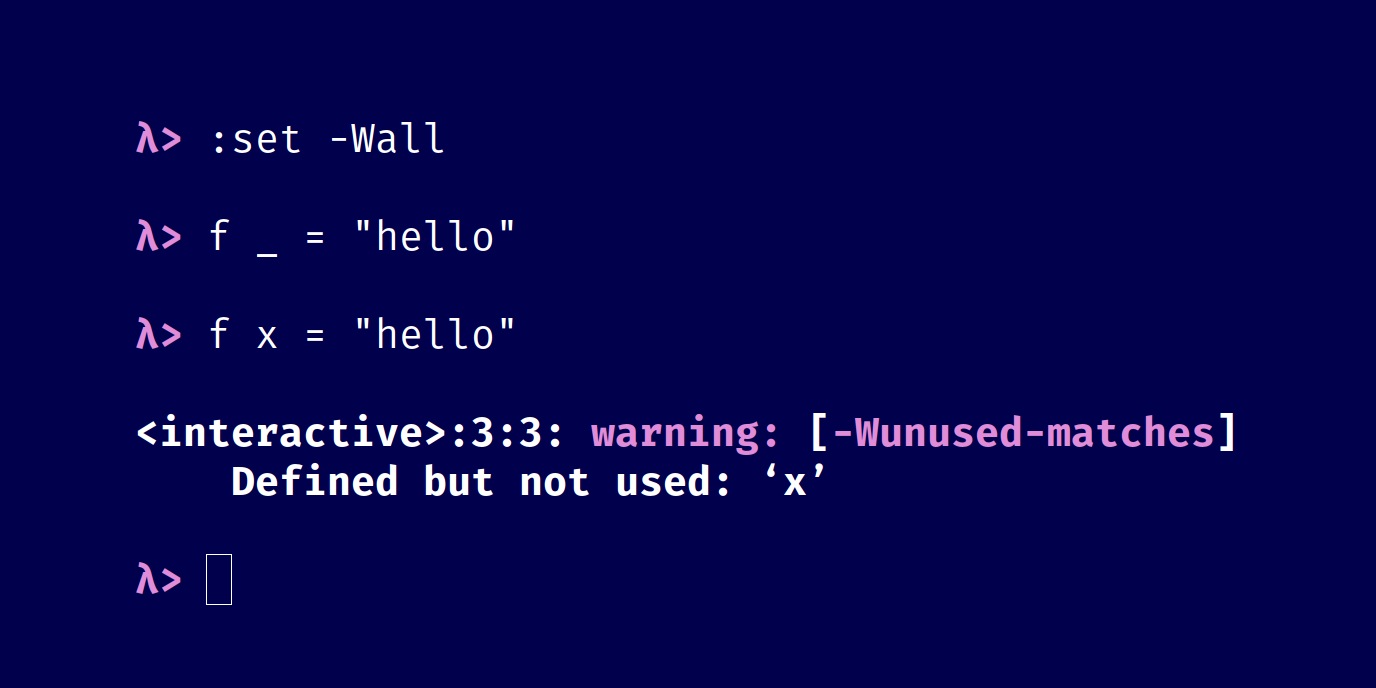
The compiler will issue a warning about an unused definition because it is likely a sign of a mistake. Using an underscore as the first character in a value-level identifier conventionally signifies that the value is unused, which suppresses this warning.

Haskell has a type called Dynamic which resembles a dynamically-typed variable in some other languages. Dynamic is a sort of wrapper that can hold a value of any type.

Haskell has a convenient notation for writing numeric ranges. It also works with a lot of types other than numbers, including types that you define yourself.

The compiler does its best to tell us when something seems amiss in our code. Let’s intentionally introduce a “mistake” and see what happens.

The GHC language extension called ExplicitForAll enables one fairly small, albeit useful, addition to Haskell’s syntax for writing type signatures: the ‘forall’ keyword. You don’t often need to be concerned with enabling this extension, because if you need forall, it’s probably because you’re using some other extension that enables it automatically, such as ScopedTypeVariables or RankNTypes.

The dollar sign infix operator is a kind of identity function with funky fixity. Here we discuss its most common usages and how to read them as well as some related functions that also use the dollar sign motif.

A short guide to the intercalate function and how it differs from intersperse. intercalate takes a list of a as its first argument, intersperses that list of a between the other lists in a [[a]], and concats the resulting list of lists.

mapMaybe maps an a -> Maybe b function over a list of a values. The return values is a list of b. Any Nothing values from the application of the a -> Maybe b function will be filtered out, and the Just constructors will also be removed from the final list.

A predicate that tells you whether something is empty is conventionally named null.

The Prelude includes four functions with the same type – round, truncate, floor, and ceiling – that all might be described as “rounding” functions but are subtly distinct.

Functions named singleton construct a collection with one element.

The toIntegralSized function provides safe conversions between most types of integers.

An organized listing of the functions we’ve singled out for praise.

The functions “foldr”, “foldMap”, and “fold” are convenient ways to combine all of the elements of a list.

The functions “for_” and “for” can be used to perform simple repetitions. They are named after “for loops”, a common feature in most programming languages.

Artwork generated using Tom Smeets’s FractalArt package.

The first lesson of this series on Functor and Bifunctor begins with motivation for functors and introduces the Functor typeclass.

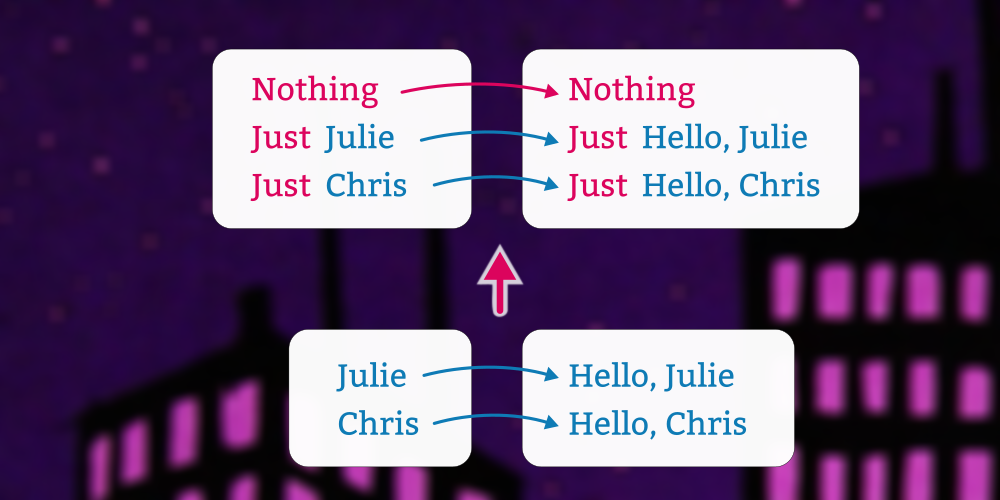
This lesson discusses Functor instances over some common product types.

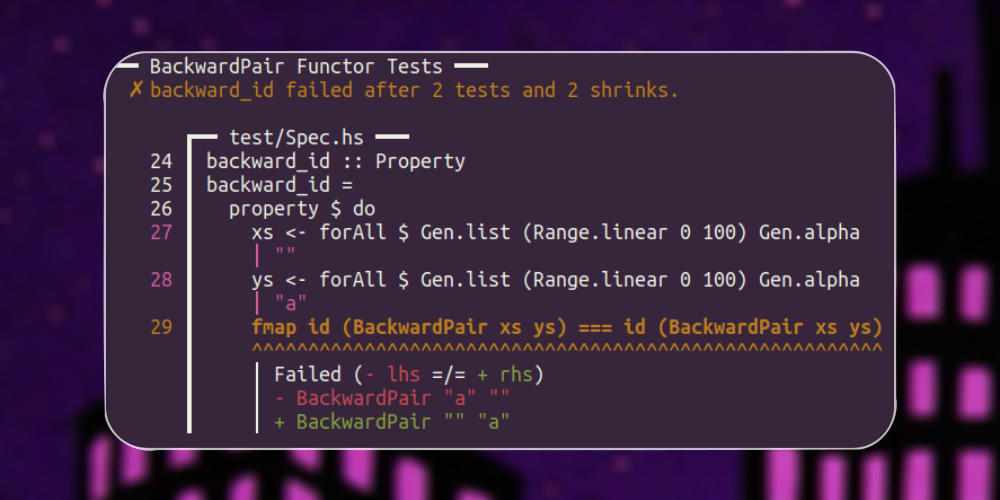
The third ‘Functor’ lesson looks at some less common cases of ‘fmap’ and discusses why some types that are functors aren’t ’Functor’s.

The fourth lesson of the ‘Functor’ series discusses Functor laws and using hedgehog to property test instances.

Here we return to some type constructors from earlier lessons, such as Either and tuples, and examines what to do when you want the possibility of mapping functions over either or both type arguments, thus introducing the class Bifunctor by example.

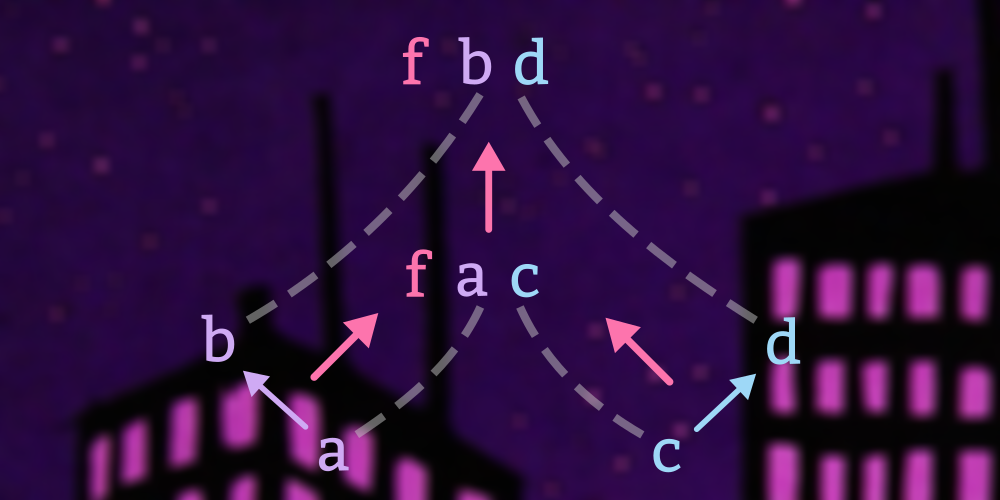
To continue our discussion of bifunctors, we look at a type that combines the bifunctorial power of sums and products in a single type and examine a typeclass that leverages that type for safe zipping of containers of unequal size.

In the previous lesson we looked at an interesting bifunctor, but in this lesson we’re going to come back to the Data.Bifunctor module and its laws. The Bifunctor laws are closely related to the Functor laws which we have already seen, but there are some interesting new things to look at here.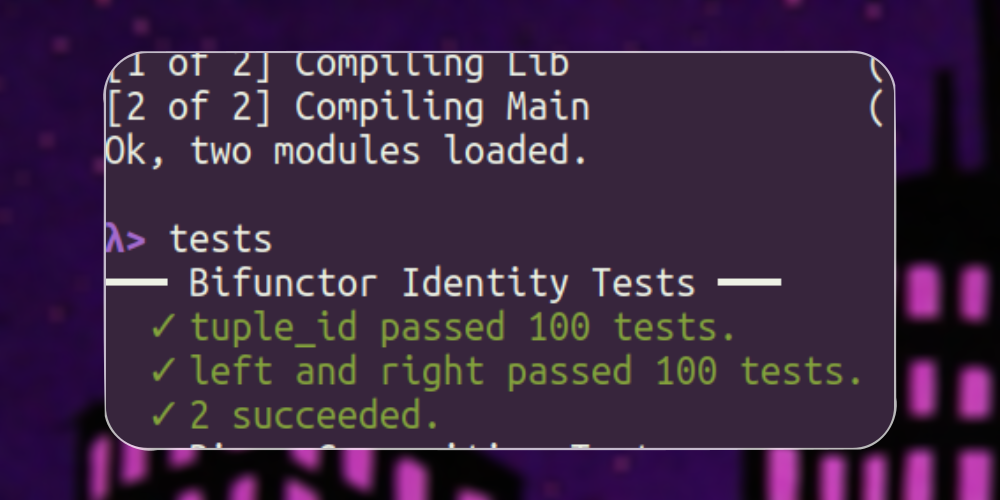

This series covers the ‘Applicative’ typeclass. After thoroughly treating several practical examples and some important applicative functors, we look at the laws of the class and property testing them with ‘hedgehog’.

This series gives a detailed explanation of the two most basic functor typeclasses, including examples of usage, and their laws. It also introduces using the ‘hedgehog’ library for property testing.

The GADTSyntax extension allows you to write data declarations so that the types of the constructors are made more obvious. This is a great reminder while you’re learning. The name “GADT syntax” comes from the fact that it was introduced for the purpose of defining GADTs, but you don’t need to worry about what GADTs are to use the syntax.

An organized listing of the GHC extensions to the Haskell language.

The :browse command in GHCi displays the contents of a module.

The :info command for GHCi isn’t the most glamorous thing in the world, but when you need information about a named entity in Haskell, it gets the job done. It generally takes one argument, which can be nearly anything that has a name. This article covers its use for a variety of things, including functions, types, and classes.

The :main command in GHCi runs your program’s “main” action. But did you know that you can also pass it command-line arguments, that the action doesn’t have to be named “main”, and that you can do the same thing using the ‘withArgs’ function?

The :print command in GHCi prints a value without forcing any evaluation. This is useful for experimenting to find out which parts of a data structure are evaluated.

The :set command can be used to change various behaviors of GHCi from within a running REPL. Options set with the :set command can be undone with the :unset command.

GHCi’s :type command can be used to ask for the type of a data constructor or function, whether from your own source file or from any dependency, so long as it is in scope. The :kind command is similar to :type but is primarily used for querying information about type constructors.

In your GHCi configuration (sometimes called your “dot ghci file”), you can write GHCi commands that will run automatically every time you start GHCi.

The Haskell REPL, GHCi, is a great interactive development tool with a lot of features. This series explains some aspects of GHCi that are not always obvious and brings some of those features to light.

Apart from the fiddly distinction regarding return type polymorphism, a major difference between an “algebra” and an “interface” is that algebras tend to be descriptive, and interfaces tend to be more prescriptive.

Often, you want typeclass instances for a newtype that are exactly the same as the instances of the underlying type. The GeneralizedNewtypeDeriving extension provides a convenient way to do that.

Haddock is the documentation tool for Haskell.

For a type to be used in a HashSet or as the key in a HashMap, the type must implement the “hash” method of the Hashable typeclass.

This section covers topics that aren’t about the Haskell language itself, but about software that helps you be more productive with it.

The Haskell Phrasebook is a free quick-start Haskell guide comprised of a sequence of small annotated programs. In accordance with tradition, we begin with a tiny example program that prints a friendly greeting.

History of the ScopedTypeVariables GHC language extension.

You can use a combination of ScopedTypeVariables, PartialTypeSignatures, and typed holes to explore code, whether it’s code you’re trying to write yourself or a new library or codebase you’re trying to learn.

There is no “universal way to print anything” in Haskell, but there is usually something you can do in this situation. Here we discuss a variety of ways to print a value if there isn’t a Show instance available.

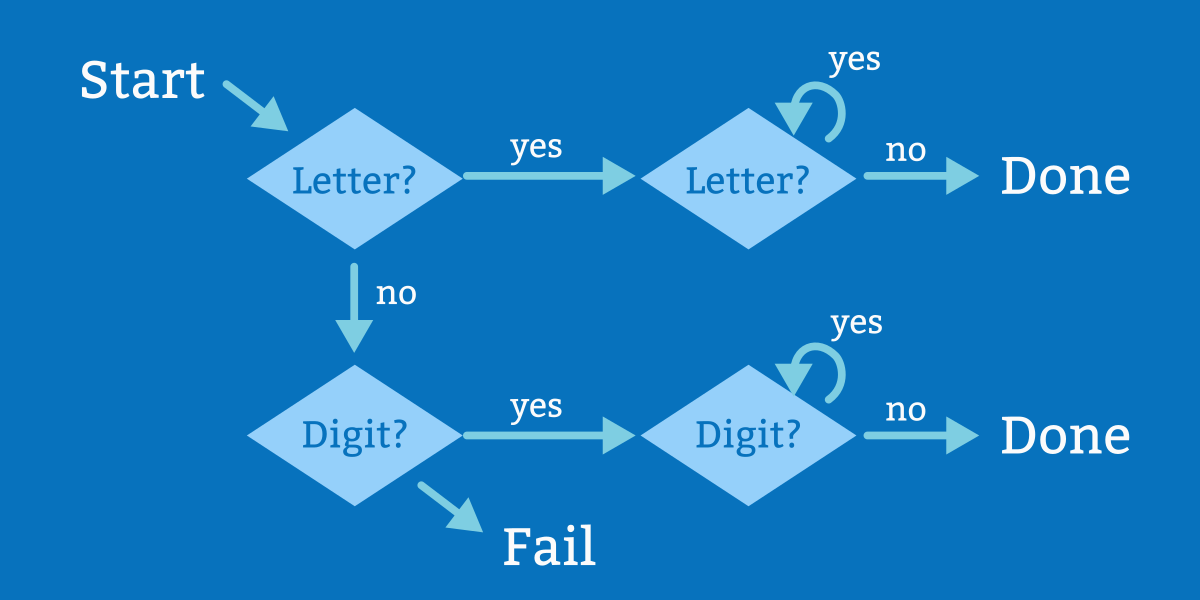
There are two kinds of names in Haskell: “Identifiers” and “operator symbols”. An identifier starts with a letter or underscore and consists of letters, numbers, underscore (_), and single quote (’). An operator symbol consists entirely of “symbol or punctuation” characters.

This continuation of the previous article comparing JavaScript and Haskell goes more deeply into implementations of the ‘minimum’ and ‘maximum’ functions. We will start by looking at how the notion of an identity value can be generalized, first by imposing a boundary on a type and later by exploring other ways to provide default return values. Finally, we’ll look at the real exception-throwing Haskell and some safer alternatives.

Branching conditionals can be written straightforwardly using the if-then-else syntax in Haskell. Note that all three are keywords and that each branch of an if-then-else expression must return the same type.

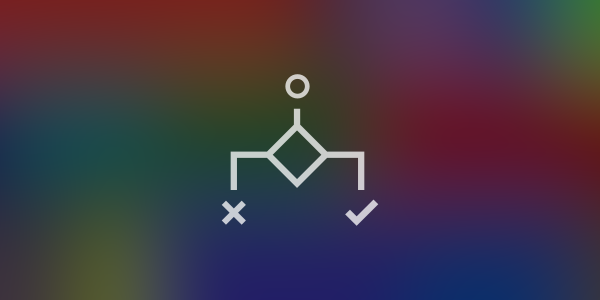
The InstanceSigs extension enables explicit type signatures as part of typeclass instance declarations. This extension is safe, and it is helpful for learning and writing code incrementally. The explicit type annotations it allows may also be useful, as explicit type annotations generally are, as documentation and for readers. The InstanceSigs extension first appeared in GHC version 7.6.1.

GHC Haskell has an overwhelming number of language extensions. Some are well documented, others are sparsely documented; some are common, others are exotic. It can be difficult terrain to navigate. Most programs can be written in vanilla Haskell with no extensions enabled. The extensions do not change the languages or its semantics. They are compiler extensions and change the way the compiler does its job, the way it reads the code. Hence, if you are using a compiler other than GHC (or are using a very old version of GHC), you may not have access to any of these extensions or only to some subset. Here we covers the extensions we think are most likely to be useful and helpful to the Haskell beginner or early intermediate as well as a few having to do with issues that crop up whether you’re ready for them or not. Each has a link to a longer article about it, describing it in more detail.

An introduction to the Haskell REPL.

Often we need a pair of conversion functions: one to encode a value as a string, and another corresponding function to decode a string back into the original type. Here we show a concise way to define these functions for datatypes whose constructors enumerate a small fixed set of possibilities (sometimes described as “enums”).

The LambdaCase GHC extension introduces a kind of expression that is something of a cross between a case expression and a lambda.

Nix is a general-purpose build tool, like a modern reinvention of Make that uses file hashes instead of timestamps. As Haskell fans we love it because the configuration language, a (mostly) pure lazy lambda calculus, has a familiar feel.

One way to observe our software’s behavior is to write programs that emit a message each time some noteworthy event occurs. Appropriate strategies for logging vary with the needs of a particular application, but our example here represents one possible design. This example also shows how to throw, catch, and log an exception.

When you enable the MagicHash GHC extension, two things change: First, the identifier naming rules are modified slightly so that names ending with one or more hash (#) characters are valid identifiers, which normally wouldn’t be allowed. Second, you can now write “unlifted literals” such as 3#.

A collection of articles highlighting Haskell libraries that generate art.

Here we demonstrate getting the current time, comparing two moments in time, and converting between a few different timestamp representations. None of the code here involves time zones. This program will not display the same current time as the clock on your wall, but it will behave the same regardless of what part of the world it runs in. This makes the types in this example suitable for a “machine” view of time such as you might use for recording the times of events in a log file, or for scheduling tasks in a multi-threaded or distributed application.

A monoid is a type together with a binary operation and an identity or neutral element. The operation must be “closed”, meaning its output has the same type as its operands, and it must be associative. The identity element must be a member of the same set and act as a neutral element with regard to that operation. Many sets have more than one such operation over them. Integers, for example, are monoids under both a “sum” and a “product” operation.

When you don’t specify a type for an expression, Hindley-Milner infers the most general, maximally-polymorphic type that your expression could possibly have. The designers of Haskell deemed that in some circumstances this leads to particularly unintuitive results, and so they invented a monomorphism restriction rule that places some limitation on the situations in which the compiler is allowed to infer a polymorphic type.

The MultiWayIf extension introduces a kind of ‘if’ expression that allows more than two branches, using the same syntax as pattern guards.

A TVar is a variable whose value can be changed. Reading a TVar gets its current value, and writing a TVar assigns it a new value.

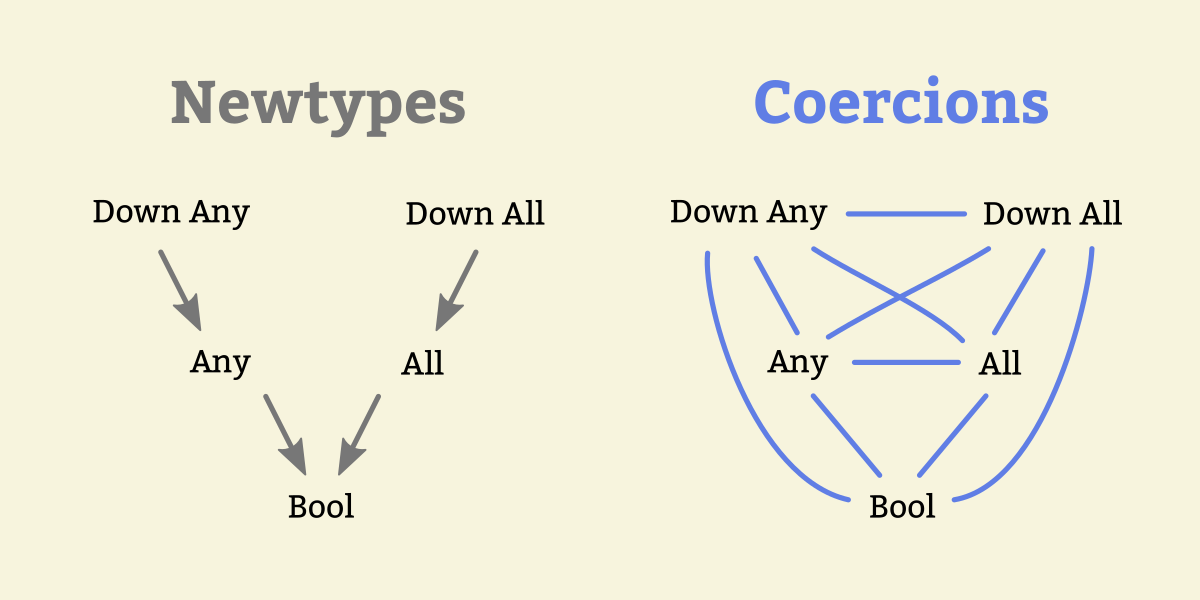
The ‘newtype’ keyword allows us to define a new type that has the same runtime representation as another type. This can become more cumbersome as the code grows more complicated or as we add more layers of newtypes. Fortunately, GHC gives us some tools that help us express trivial type conversions more easily. The ‘coerce’ function can convert between two types A and B as long as the constraint Coercible A B is satisfied.

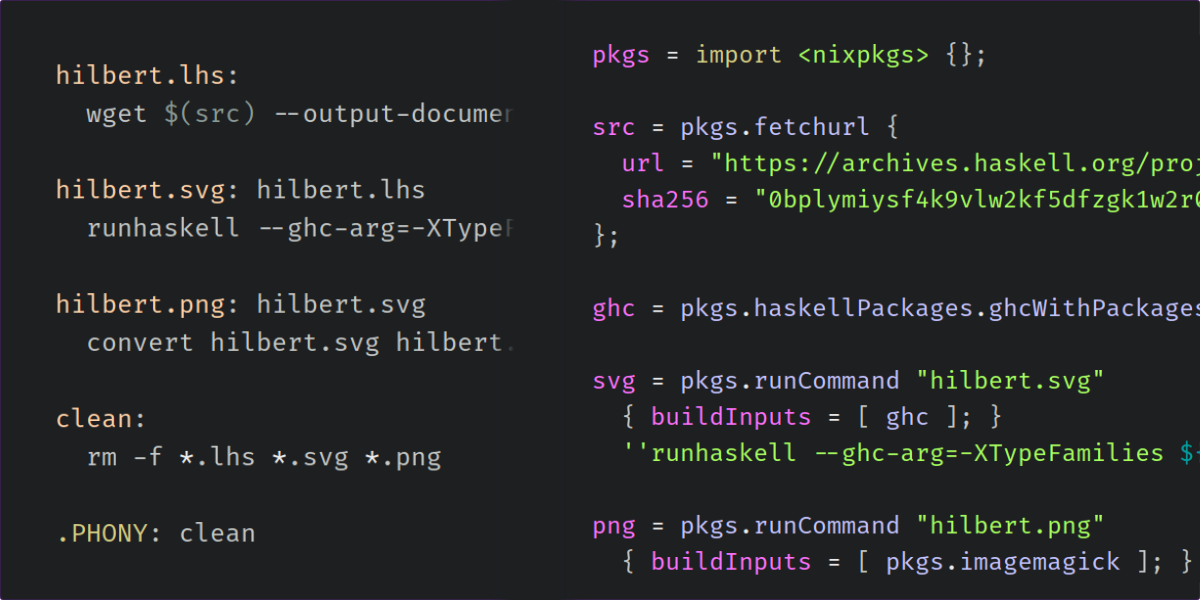
The ‘nix-build’ program can serve as a good alternative to GNU Make. In this lesson, we first write a Makefile that downloads some Haskell code and runs it to produce an image. Then we rewrite the Makefile using Nix to compare and contrast the two approaches.

The NoImplicitPrelude GHC extension is used to disable the implicit importing of the Prelude module.

The NoMonomorphismRestriction extension and its sibling, MonomorphismRestriction, enable you to control a specific quirk of the type inference system: the monomorphism restriction.

White space is syntactically significant in Haskell, and the parser can be persnickety about indentation. Many beginning Haskellers have been frustrated by parse errors and the difficulty of determining just what went wrong. Here we present an introduction to how Haskell uses indentation and white space.

With the NumericUnderscores GHC extension enabled, you may place underscores anywhere within a numeric literal. The compiler ignores the underscores, but they may help provide visual guidance to human readers when numbers are large. For example, one million (1,000,000) normally would be expressed in Haskell as 1000000. With NumericUnderscores, it may be written as 1000000 instead.

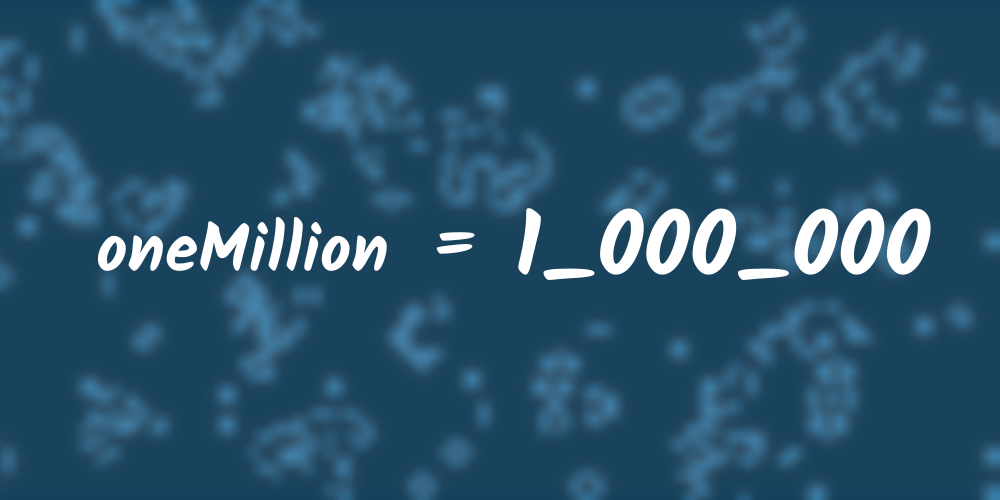
JavaScript has a handful of builtin infix operators and some convenient tricks you can do with them. Here we look at what you can do with those operators, and how you can do the same things in Haskell.

OverloadedStrings is one of the most commonly-enabled GHC extensions. Normally, string literals always have the type String, which is a type alias for [Char]. The OverloadedStrings extension makes string literal syntax more general, allowing string literals to denote values of types other than String.

There are a lot of parsing libraries in Haskell. What’s more important to you: Giving informative error messages for invalid inputs, or speed? Do you need to run the parser incrementally? Do you want automatic backtracking?

In standard Haskell without the PartialTypeSignatures GHC extension, type inference is a somewhat all-or-nothing affair. You can either omit the type signature for a function and let the compiler infer it, or you can write a type signature yourself. But what if we want to only specify part of the type and let the compiler infer the rest? The PartialTypeSignatures extension, available in GHC 7.10 and later, can help.

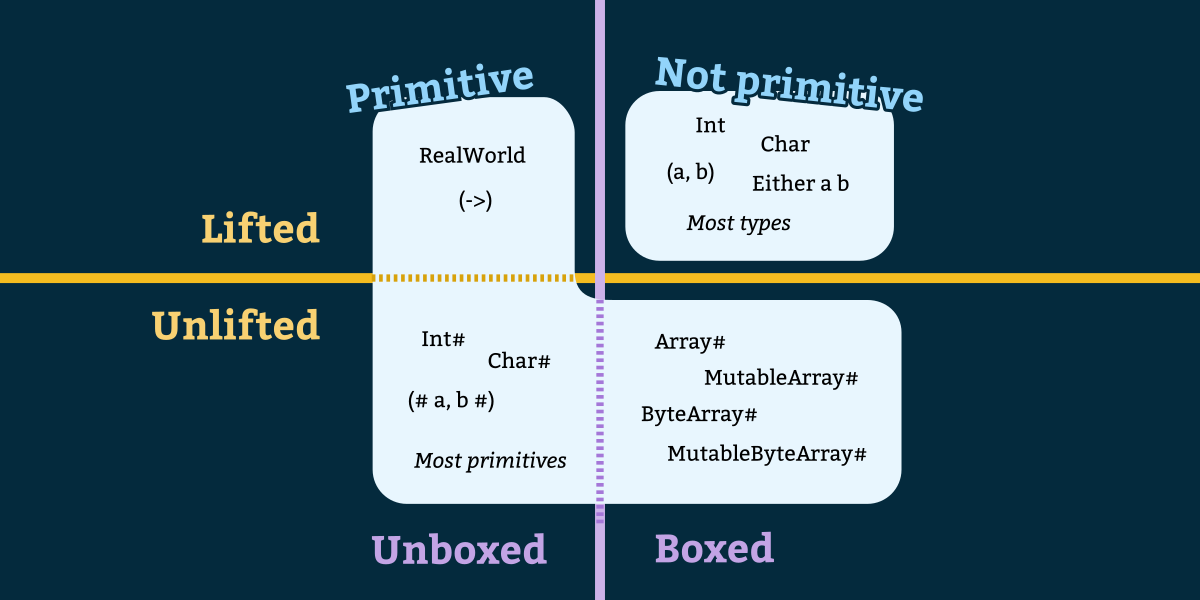
An explanation of the different kinds of types in GHC Haskell, including the differences between primitive, unlifted, and unboxed types, the MagicHash language extension, and the meaning of levity polymorphism.

The itertools.accumulate function gives a running total. A function that produces this sort of running total in Haskell is called a scan. There are a bunch of scan functions; the one that corresponds most closely to itertools.accumulate is called “scanl1”.

The primary role of a Python data class is to simply hold the values that were passed as constructor arguments. This feature strongly resembles Haskell datatypes, particularly when we use Haskell’s record syntax.

In constrast with the ‘takewhile’ function which stops the first time it encounters a non-matching value, ‘filter’ continues past non-matching values and produces a list containing all of the values that satisfy the predicate. We also discuss the itertools ‘compress’ function, and give four different Haskell implementations of this function using tools we have seen previously.

Decorator syntax refers to some syntactic sugar in Python that lets you simultaneously define a function f and apply a function g to the function you just defined. f is called the “decorated” function, and g is called the “decorator.” Here we look at several examples using decorators in Python, compare them to similar situations in Haskell, and discuss how lambdas let us achieve the same result without having a special syntax for decorators.

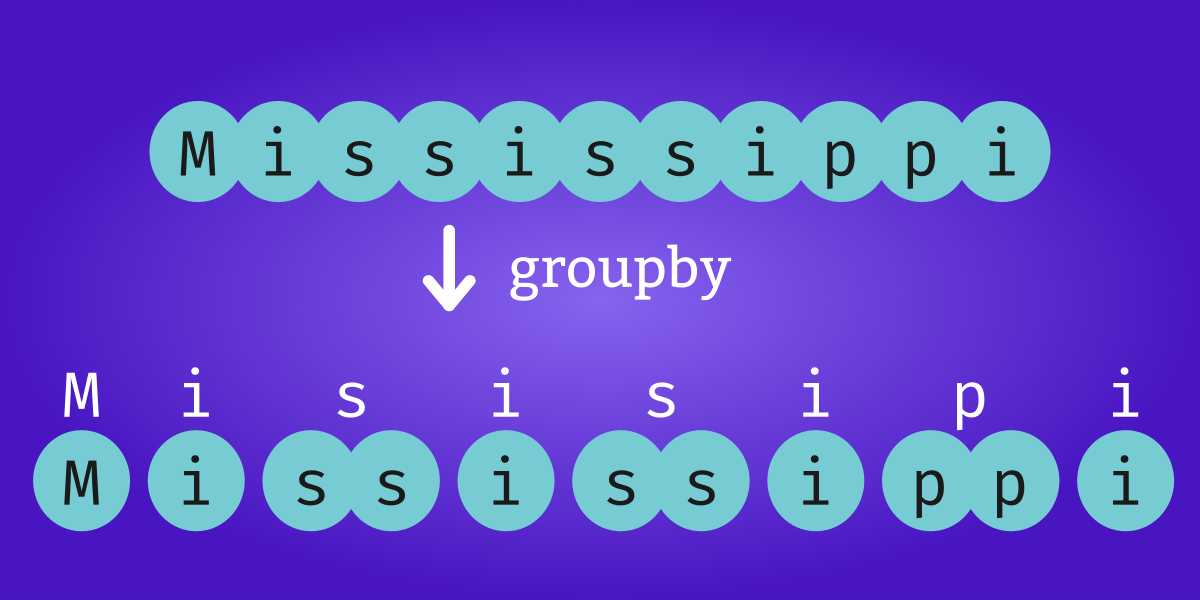
The itertools ‘groupby’ function divides a sequence into contiguous subsequences where the elements in each subsequence share something in common. Haskell’s ‘groupBy’ function is similar.

This lesson is about functions that produce simple never-ending iterators. The ability to represent concepts like “counting upward from one” and “repeating an item indefinitely” is a big part of what distinguishes iterators from lists in Python. In Haskell we describe things like Python iterators as “lazy” because elements are not evaluated until they are needed. Python lists, in contrast, we describe as “strict”.

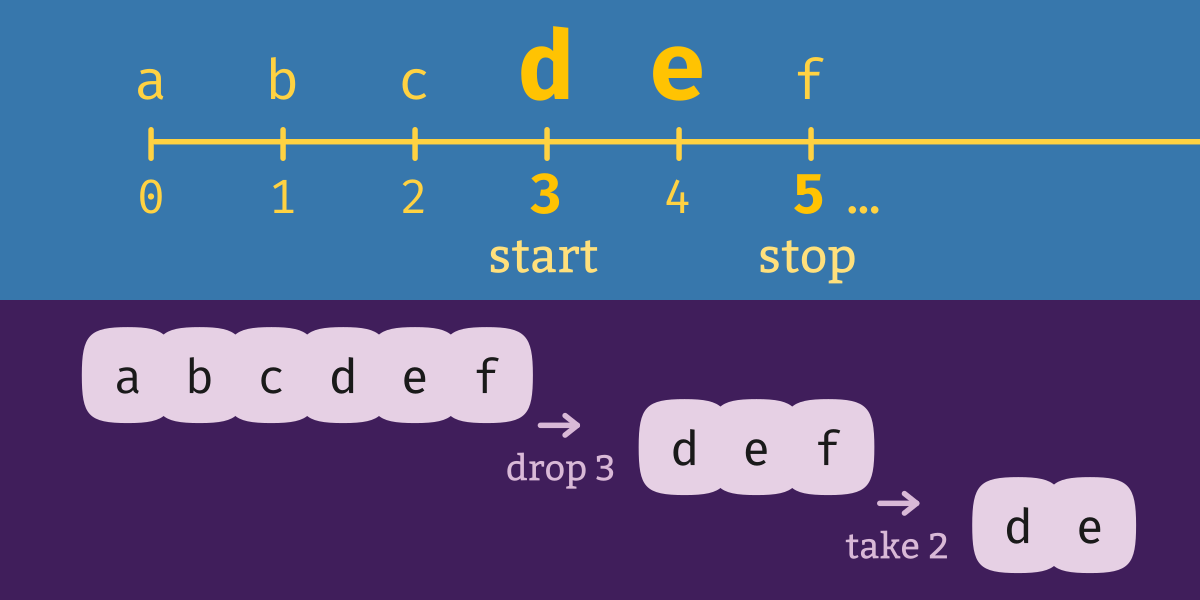
We previously discussed how Python iterators relate to Haskell lists. If you’re familiar with the ‘itertools’ module, these next lessons will help you get started quickly with Haskell’s ‘Data.List’ module. We begin with a discussion of ‘islice’.

A Python iterator is a sort of sequence that, unlike a list, computes each subsequent value only as it is needed rather than computing the entire list all at once. In simple cases, Haskell’s list type ([]) fulfills a similar role. This series compares Python iterators to Haskell’s list datatype, taking a deep dive into the itertools library and the corresponding functions in the Haskell standard library.

To concatenate two Python iterators, we use ‘itertools.chain’. The resulting iterator consists of each element from the first argument, followed by each element of the second argument. The corresponding Haskell function is called (++). The ‘chain’ function is variadic; it can accept any number of arguments, not just two. This makes it easy to chain together any number of iterators without having to use nested function applications. Haskell doesn’t have variadic functions, but it does let you define infix operators, which can be used to get a similar convenient effect. The (++) function concatenates exactly two lists, but infix notation makes it easy to chain together as many concatenations as you like. If you aren’t chaining together some fixed number of lists, but rather a list of lists, you can use ’chain.from_iterable’. The Haskell equivalent is called ‘concat’.

Whereas Python’s islice (and Haskell’s take and drop) cut some particular number of elements from a list, the corresponding takewhile and dropwhile functions inspect the list’s values and truncate the list based on what it contains. take and takewhile are both ways of taking; drop and dropwhile are both ways of dropping. The difference is how they determine how much of the series to take or drop. Haskell also comes with a function called “span” which performs both a take and a drop at the same time.

Python iterators and Haskell lists are different things. We have not yet had to reckon with this fact, but for this lesson we can no longer look past the distinction. First we’ll set up an example to illustrate the problem with iterators that itertools.tee solves, then discuss the contrast with Haskell lists, and finally show how to use Python’s tee function.

If you’ve used only one of Python’s iterator functions, there’s a good chance it’s this one. ‘map’ is essential because it’s the functor operation for lists. It operates over the content of the list but not the structure of the list. This implies, among other things, that the list that map returns will always have the same number of elements as the input list.

Here we look at the closely-related Python functions zip, itertools.zip_longest, and enumerate, and the Haskell functions zip, zip3, and padZip.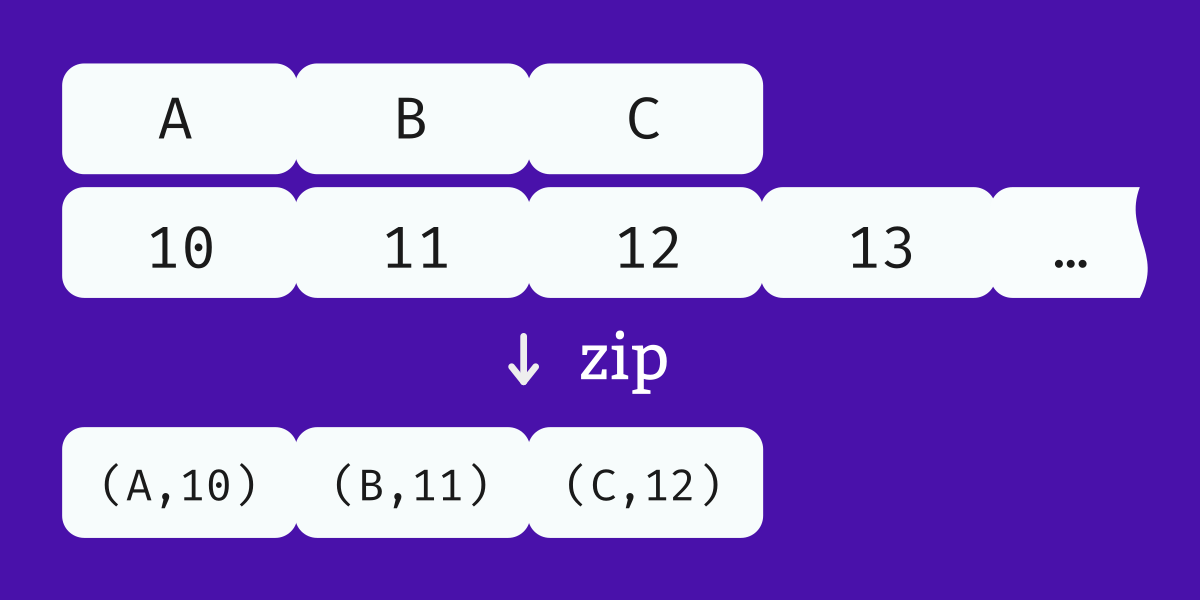

Quasi-quotation is a feature of Template Haskell, related to the TemplateHaskell language extension (although you can enable the QuasiQuotes extension without enabling TemplateHaskell, and vice versa). Some use of quasi-quotes include: 1. Evaluating expressions at compile time, such as URLs and JSON literals; 2. Adding Haskell syntax features like string interpolation and multi-line strings.

The original program was one of the first things I ever produced in Haskell, and it looks very different from something I’d write today. In this lesson, I walk through the process of cleaning it up, thinking carefully about what makes a well-designed program.

The phrase “rigid type variable” shows up in several contexts in GHC error messages. Often, when it appears, it’s in a context where you know that the type variable it refers to is totally unconstrained, or parametrically polymorphic, and you may have found yourself wondering what is exactly is meant by “rigid”? How can something that could be anything be “rigid”? The phrase “rigid type variable” can be traced back at least to 2004, to a paper contrasting rigid types with “wobbly types”, that is, types that the compiler has to guess at. A later paper, published in 2006 suggested that the other name considered for rigid type was “user-specified type.”

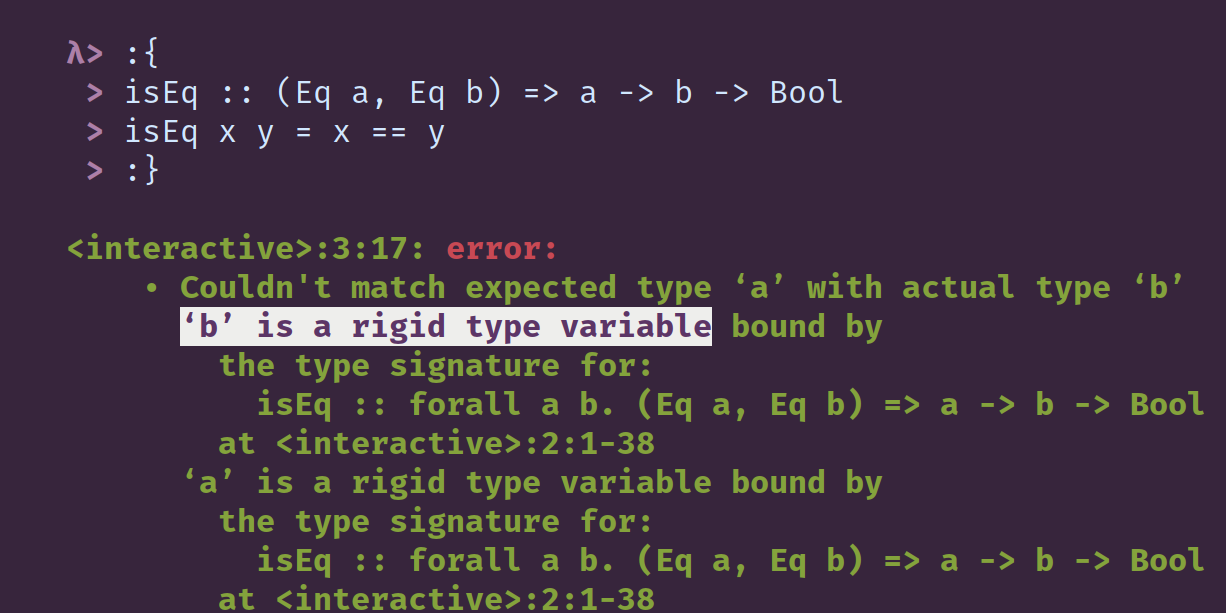
ScopedTypeVariables allows local type signatures to reference type variables from their enclosing context. This extension first appeared in GHC 6.8.1, and it implies the extension ExplicitForAll.

A semigroup is a type together with a binary operation. The operation must be “closed”, meaning its output has the same type as its operands, and it must be “associative”: x <> (y <> z) = (x <> y) <> z. Many sets have more than one such operation over them. Integers, for example, are semigroups under both a “min” and a “max” operation.

A semiring is like a double monoid. That is, it’s a set equipped with two binary associative operations ⊕ and ⊗. The “addition” operation ⊕ is commutative, and its identity value is the annihilator for the “multiplication” operation ⊗. One familiar example is integers: Addition and multiplication are monoids, and the additive identity (0) is the multiplicative annihilator. We also look at some that might be less familiar but are also relevant to programming.

Here I consider ways of speeding up the tweet-processing program by rethinking the types and structure of the previous versions.

In many cases, Stack and Nix are considered competing tools rather than complementary ones. However, there are circumstances in which you want them to learn to play nice together. If you find yourself in that situation, here are some tips from the trenches, as it were, on using Stack’s Nix integration.

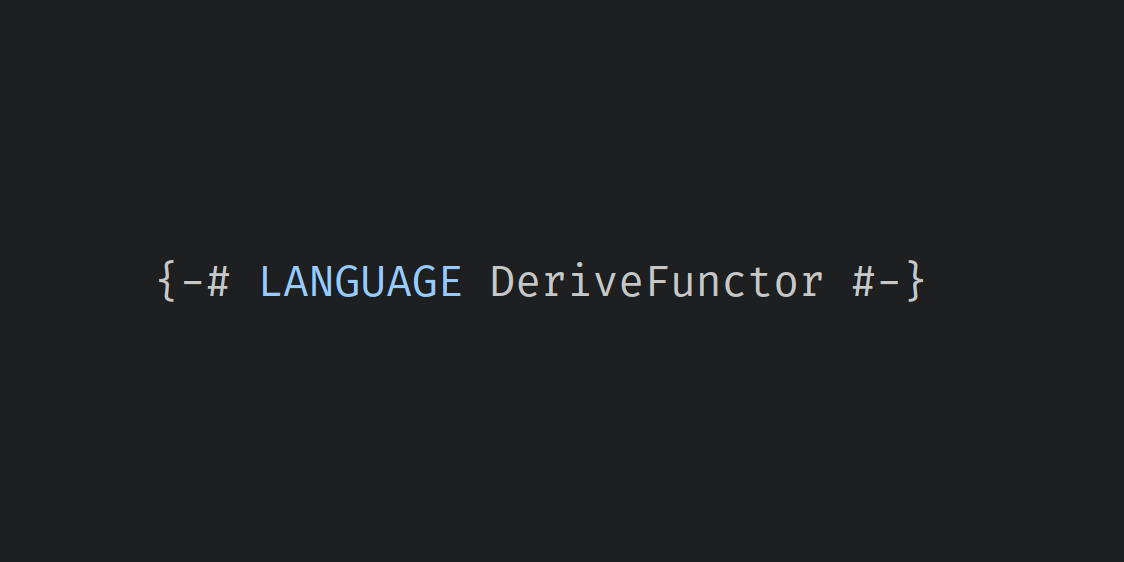
These GHC language extensions extend the deriving mechanism specified in the Haskell Report by enabling automatic deriving of specific additional classes: DeriveFunctor, DeriveFoldable, DeriveTraversable, DeriveGeneric, DeriveLift, and DeriveDataTypeable.

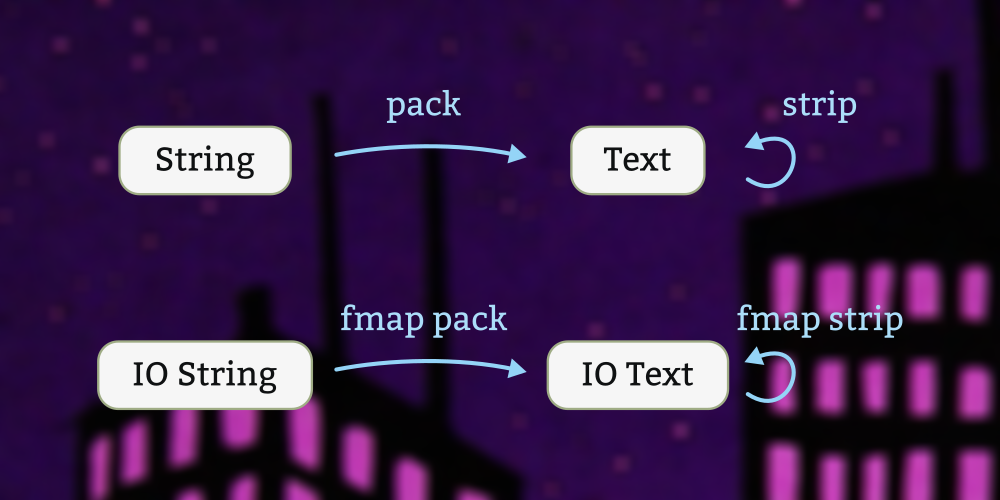
Here we look at two common Haskell libraries, text and bytestring, and addressing the frequently-asked question: “Why are there so many types of strings?” We’ll examine the differences between various string types, talk about what situations in which each is appropriate, and see what functions the libraries give us to convert among them.

For our four-year friendversary, I rewrote Chris’s original program that mines his tweet history for when and how our friendship began, using a different CSV library and ending up with a slightly surprising result.

‘Template Haskell’ is the name of both Haskell’s entire metaprogramming infrastructure as well as a specific GHC extension that enables a number of language features that support it. Most notably, enabling the TemplateHaskell extension allows you to write “splices”, that allow you to inject generated code into your code.

GHC is the Haskell compiler. In addition the compiler, GHC also includes a REPL called GHCi (“GHC interactive”), an executable called runghc to run Haskell source files directly without a compilation step, and a great number of extensions to the Haskell language which can enable features beyond what is given in the Haskell language specification.

The Haskell Phrasebook is a free quick-start Haskell guide comprised of a sequence of small annotated programs. It provides a cursory overview of selected Haskell features, jumping-off points for further reading, and recommendations to help get you writing programs as soon as possible.

The course begins with two lessons on case expressions to ensure a solid foundation. From there, we write three functions for checking that inputs are valid passwords according to the rules of our system. The rest of the lessons iteratively expand on and refactor those functions into a small program that validates usernames and passwords, constructs a User if both are valid inputs, and returns pretty error messages if they are not. Along the way we learn about Monad and Applicative and how they are similar and different and how to use types to rethink our solutions to problems.

Four years later, we revisit a CSV processing project to think about what we might have done differently if we were writing it today. Could it be written more clearly? More efficiently? With other parsing libraries? Are there other interesting things we could learn from the data? Come join us on a trip through the design space and down memory lane.

First we discuss “visitor pattern” and see some examples in Java, and then we look at comparable code in Haskell. We will see that the Java code using visitors bears a strong resemblance to what we call “sum types” or “tagged unions” in Haskell.

Threads are concurrent flows of execution within one process. Haskell chooses to implement its own multithreading abstraction instead of simply using native OS threads directly, because OS threads are slower to initialize and have a greater memory cost. For applications written entirely in Haskell, there is no semantic difference between OS threads and Haskell threads, but there are some reasons to appreciate the distinction between the two. By default, Haskell programs only use a single OS thread. You must build with the -threaded flag to enable multiple OS threads.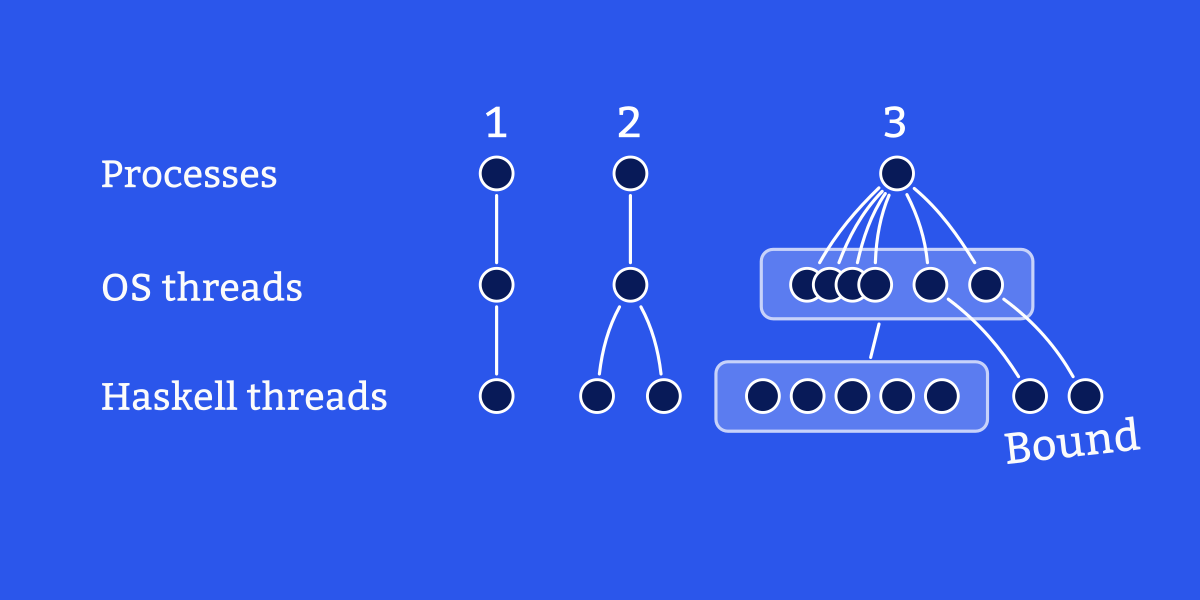

Threads are subroutines that can run concurrently. Every Haskell program begins with one thread, called the main thread. Starting an additional thread is called forking a thread.

For everyday programming, complexity comes down to five words: constant, logarithmic, linear, polynomial, and exponential.

When a program requests some information from an external source (say, from a web server) we usually want it to give up after some amount of time instead hanging indefinitely awaiting a response that may never arrive.

The Native GUI Clocks course will feature lessons for building native clock applications with several different Haskell GUI libraries. Lessons will use different libraries in order to highlight different aspects of them.

The first Timepieces lesson covers setting up an initial project with fltkhs-themes and using implicit parameters.

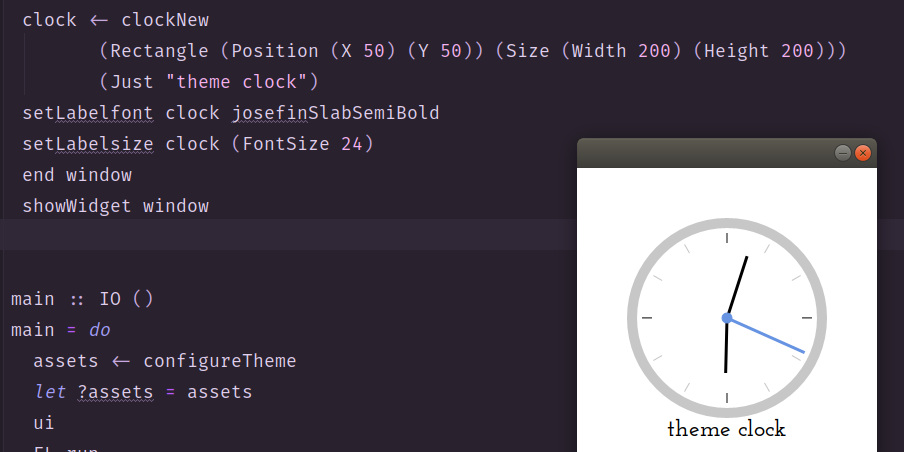
This lesson covers building a very simple GUI application with GTK+ using the ‘gtk3’ Haskell package. We create an application that consists of a GTK Window which contains a Frame, which in turn contains a DrawingArea. In that drawing area, we use Cairo and Pango to render text. Finally, we use the ‘linear’ Haskell package for the calculation that we need to center that text within the drawing area.

Now that we’ve got our basic application up and running with ‘gtk3’, we turn our attention to setting the time that our clock should display. We use the ‘time’ package and transactional variables (TVar) from the ‘stm’ package to achieve this. By the end, we have our clock showing the right time and rendering nicely in the window.

An interesting aspect of using the fltkhs library is how un-Haskelly it is. The library is designed to adhere as much as it could to the structure and naming conventions of FLTK. So, to understand how some of its types work and how to interpret its documentation, we needed to understand FLTK’s hierarchies and documentation a bit better than we did last time. This time we are making a window resizable as an excuse to understand which things inherit from what.

Each block of code inside the ‘atomically’ function is a transaction. When you read and write TVars within a transaction, you are shielded from the effects of any other threads that may also be messing with the variables concurrently. In celebration of how transactional variables free us from a lot of messy concerns that usually complicate concurrent programming, here is a classic demonstration that simulates passing money around between bank accounts.

We walk through a common use case for the ‘transformers’ library and use it to illustrate type aliases, newtypes, and various approaches for typeclass deriving, using the GeneralizedNewtypeDeriving and DerivingVia GHC extensions.

Haskell resources for Java programmers.

Haskell resources for JavaScript programmers.

Haskell resources for Python programmers.

This lesson explains what it means for data constructors to have constraints, a special constraint called type equality, written as (~), and why placing a type equality constraint on a constructor has interesting ramifications.

In standard Haskell, operator symbols may only be used at the value level. GHC expands the role of operators with the TypeOperators extension, which makes it possible to use an operator as the name of a type.

Typed holes are a useful feature of GHC Haskell that allow you to replace expressions with holes in the form of underscores. Those holes provoke GHC into telling you the type of the hole as well as a list of valid hole fits, and those help you write your code.

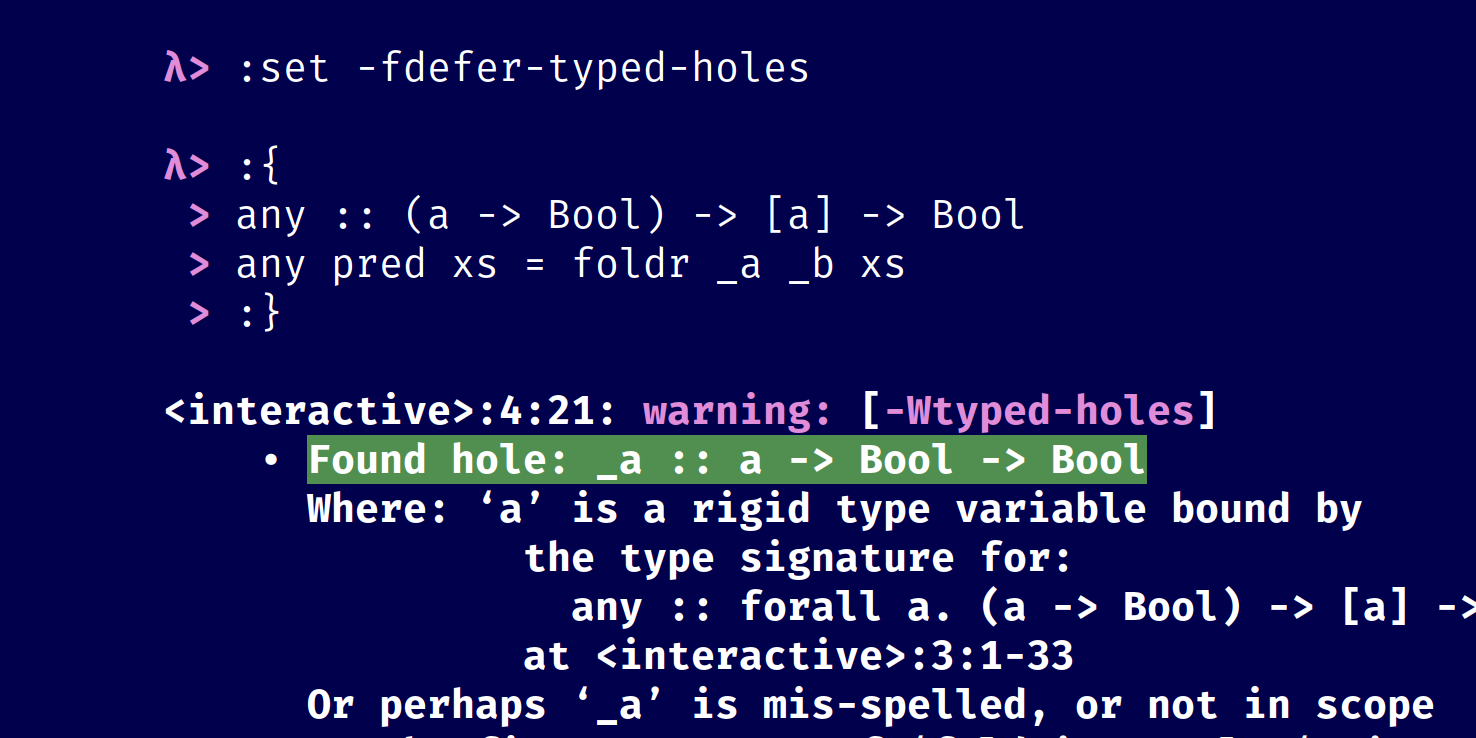
An underscore character in Haskell code usually represents something we don’t care about or don’t know about – a wildcard, a hole, or a discarded result.

The concept of contravariance, contravariant functors, and the Contravariant typeclass defined in the ‘contravariance’ Haskell library.

Profunctors are bifunctors that are contravariant in their first type argument and covariant in their second one. Make sure that you understand contravariance first. Then we just need to talk about bifunctors, and finally we will get to profunctors.

The ‘ghcid’ package is a reliable, helpful tool built on top of GHCi. It opens a project-aware REPL and automatically reloads your code on every save, so it saves you the step of manually :reload-ing. It also keeps the the top type error or warning in focus so that you don’t have to scroll up and try to find the top of the current batch as you work on fixing them. It’s really useful especially when you are refactoring or developing with holes at the type- or term-level.

Haskell has a nice REPL known as GHCi, where GHC refers to the main Haskell compiler and the ‘i’ is for ‘interactive’. GHCi and the continual typechecking tool called ghcid are useful for fast feedback loops while you code, but GHCi has a lot of other features besides. This is a very basic introduction to some of those.

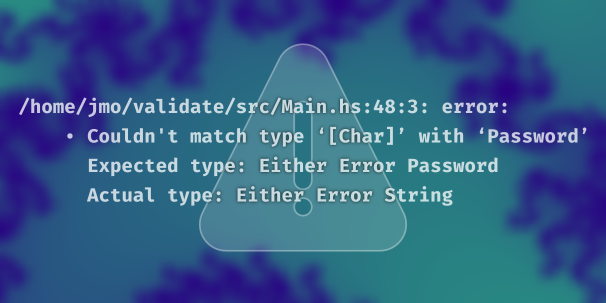
Using newtypes like Password instead of a generic string type can increase type safety and expressiveness, but, as we saw previously, it can also lead to annoyances where you have to convert between two types that are, in one sense, the same. This lesson of the Validation course introduces the Coercible class as general way of handling those conversions.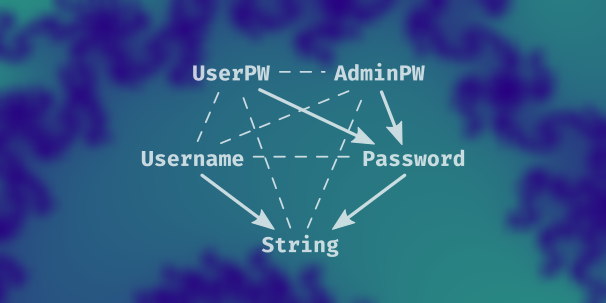

This lesson of the Validation course looks into the prisms from the validation library and how we can use them to generalize our code to be, as they say, more liberal in what we accept. Doing this requires us to look into the lens library and some of its functions, as well as take a deeper look at what it means for types to be isomorphic to each other.

The first lesson of the Validation course takes a look at conditional if-then-else expressions in Haskell and compares them to expressions with different syntax: case expressions. Conditionals and case expressions serve a similar purpose; they both allow a function’s behavior to vary depending on the result of an expression. However, case expressions have some flexibility that if expressions do not have, namely allowing behavior to branch on values other than booleans.

The second lesson of the Validation course presents an extended example of using case expressions. In particular, we look carefully at an example that pattern matches on Maybe values, since the rest of the course assumes you understand that well. Our example code checks two String inputs to see if they are anagrams of one another. Additionally, we write a main executable that asks for and accepts user inputs in the REPL and uses the anagram-checking function on those inputs.

In lesson 3 of the Validation course, we write code for validating passwords. We will write three functions. One checks a String for a maximum length. The second verifies that a String input is all alphanumeric characters – no special characters allowed in our passwords! The third will strip any leading white space off of a String input. All three return a Maybe String, so invalid inputs are all Nothing. This lesson ends with an exercise.

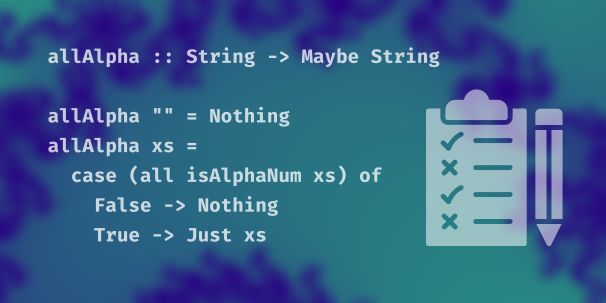
We open by looking at a couple of possible solutions to the exercise we left you with last time. We then introduce an operator called “bind”, >>=, that can be used to reduce nested case expressions. That allows us to forego the laborious pattern matching and makes for a concise expression; however, there are some drawbacks to this approach as well. Since >>= is the principle operator of the Monad typeclass, we discuss what monads are.

So far in the Validation course, we’ve had no way to distinguish between different errors (they are all Nothing) or which error is short-circuiting our program. Using Either, a sum type similar to Maybe, allows us to pass around more information about our error cases. This lesson refactors the previous lesson’s code to use Either and its Monad instead of Maybe.

In this lesson we introduce some new types. We use newtypes that will help us distinguish at the type level between strings that represent inputs (password, username) and strings that represent errors. We’d also like to keep a username and a password together as a User value, so we write a product type called User. We refactor the code we already have, write new functions that validate username inputs, and write a function that constructs a User from the conjunction of a valid Username and a valid Password.

In this lesson, we encounter a problem as we write the function to construct a User and introduce an operator from the Applicative typeclass to help us.

We do a thorough refactoring to switch from Either to Validation. Despite the fact that those two types are isomorphic to each other, their Applicative instances are quite different and switching to Validation allows us to accumulate errors on the left. Since that Applicative relies on having an instance of Semigroup to handle the accumulation, we need to write a Semigroup instance for our Error newtype.

In lesson 9 of the Validation course, we look at how to pass much nicer, easier to read error (and success!) messages along to our users. To facilitate this, we write an ‘errorCoerce’ function so that we can use list functions with our Error newtype, and then we finish the course with tidy and informative error messages.

We can use the ‘let’ keyword to give an expression a name by which we can refer to it later. Naming an expression may help clarify the meaning of code and can reduce duplication when the same expression is written more than once.

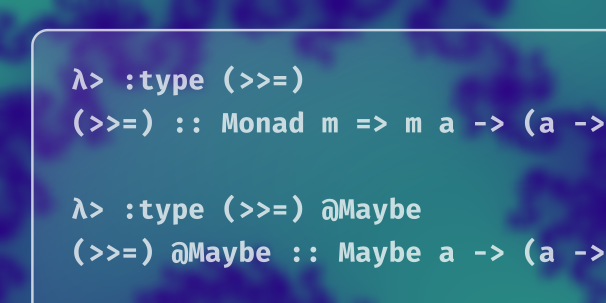
TypeApplications allows you to instantiate one or more of a polymorphic function’s type arguments to a specific type. Use the @ keyword to apply the function to a type. This has a lot of benefits both for learning and for writing code. The TypeApplications extension first appeared in GHC 8.0.

This course uses Haskell to explore what a web server is, starting from how we use sockets and the network library, and moving toward a foundation for higher-level libraries for building web applications. On the way, you will learn: what is a socket; how to read the HTTP specification; the difference between a strict ByteString, a lazy ByteString, and a byte string Builder; what “chunked transfer coding” means in HTTP, and what that has to do with lazy I/O; how to use Attoparsec to parse an HTTP request; how to use the Pipes library to parse streaming input.

The parsers we’ve written so far have been fairly straightforward transcriptions of the grammar given by RFC 7230. Parsing a message body is more involved, because: 1. There are multiple ways to encode the body, and we need to interpret the message headers first to figure out which encoding was used in the particular message we’re parsing; 2. We have to begin considering ways in which a request can be invalid other than by being grammatically malformed. In this lesson we use the Either monad to handle failure and the ‘traverse’ function to apply a function that might fail to each element in a list. As an exercise, you will write a parser for a comma-separated list with optionally quoted elements.

In this lesson we fill in the final pieces to complete the Request parser, and then we begin putting it to work. We’re going to touch the sockets again; this time in addition to writing to sockets we’ll be reading from them.

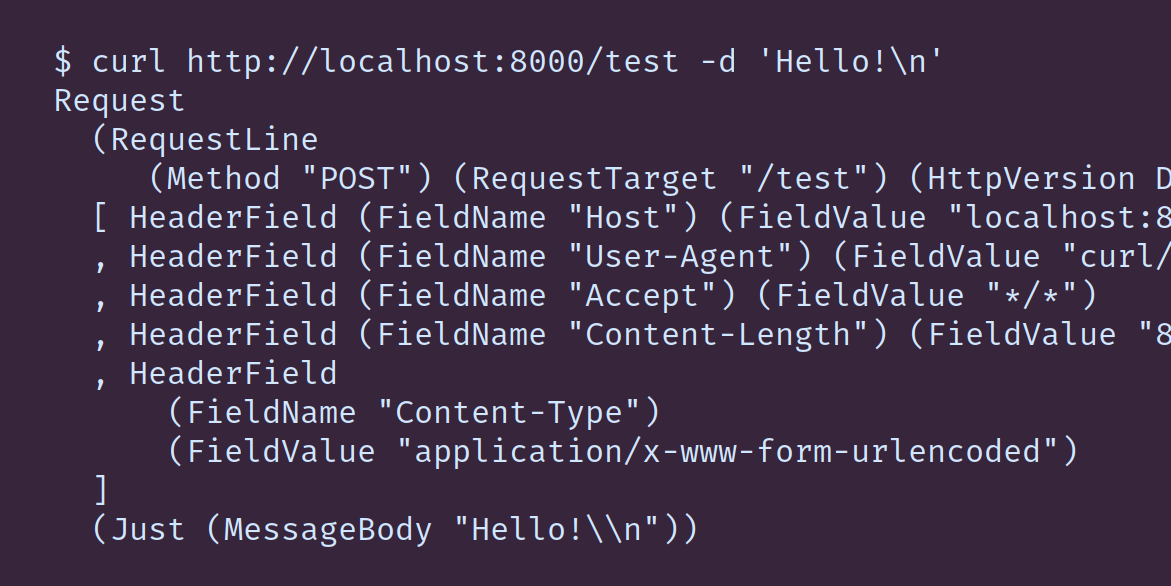
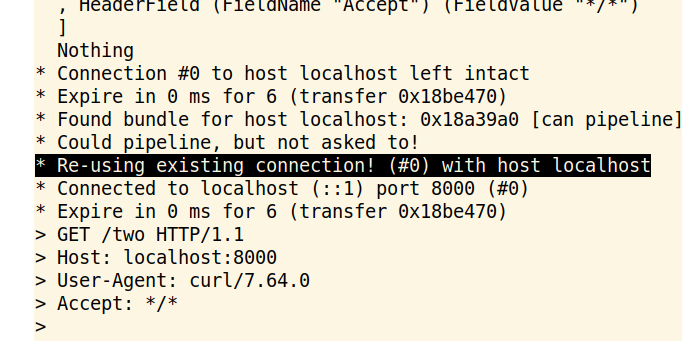
Often a client will make a series of multiple HTTP requests at once; for example, loading a webpage usually involves an initial request for the HTML, followed by a separate request for each image, stylesheet, etc. Opening and closing sockets times some amount of time, and so HTTP allows us to reuse the socket for multiple requests. In this lesson we’re going to write three more iterations of our server: First we’ll add support for connection reuse. Then we’ll rewrite it to read the input from the socket as a series of strict ByteStrings instead of representing the entire stream as a single lazy ByteString.

Using Attoparsec’s incremental parsing ability, we fed the parser small chunks at a time. This approach eliminates the lazy I/O and affords us some more manual control over the I/O at the expense of being slightly more cumbersome. A streaming library like pipes provides a good middle ground between the two approaches, giving us back some of the convenience of lazy datatypes – and some additional ability to decompose our code into smaller cohesive pieces – without sacrificing fine-grained control over the operations of the program.

The concept of a socket forms the core of the Unix networking library. This lesson sets up a foundation for the Web Servers course by introducing sockets and the Haskell network library.

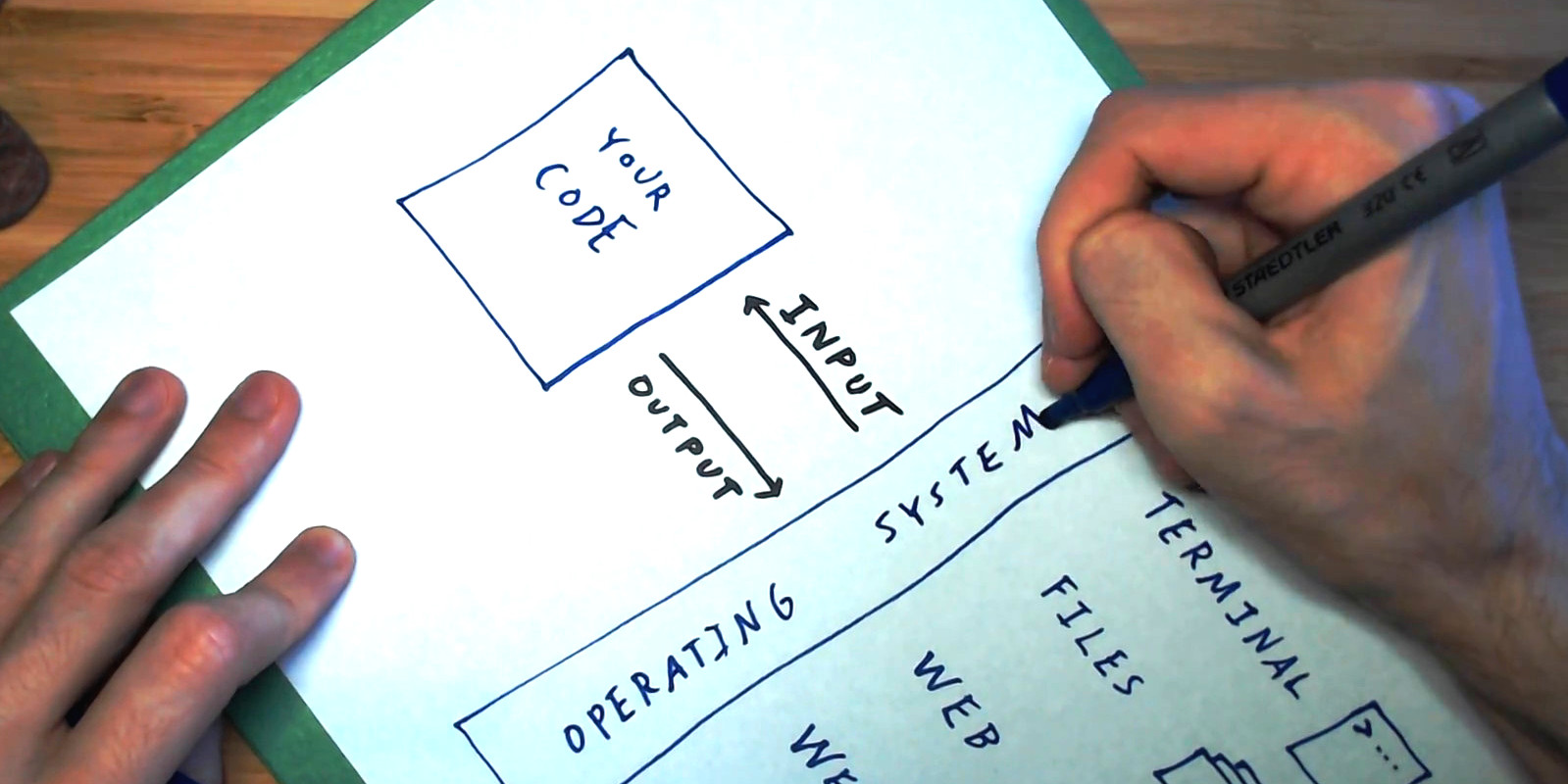
We know we’re going to be reading some bytes from this socket and writing some bytes to this socket, but how do we format those so that the client and server can understand each other? We need some common language that they both speak in order for these bytes to have any meaning. In the context of networking, we call such a language a ‘protocol’, and the one we’ll be talking about here is HTTP, which stands for Hypertext Transfer Protocol.

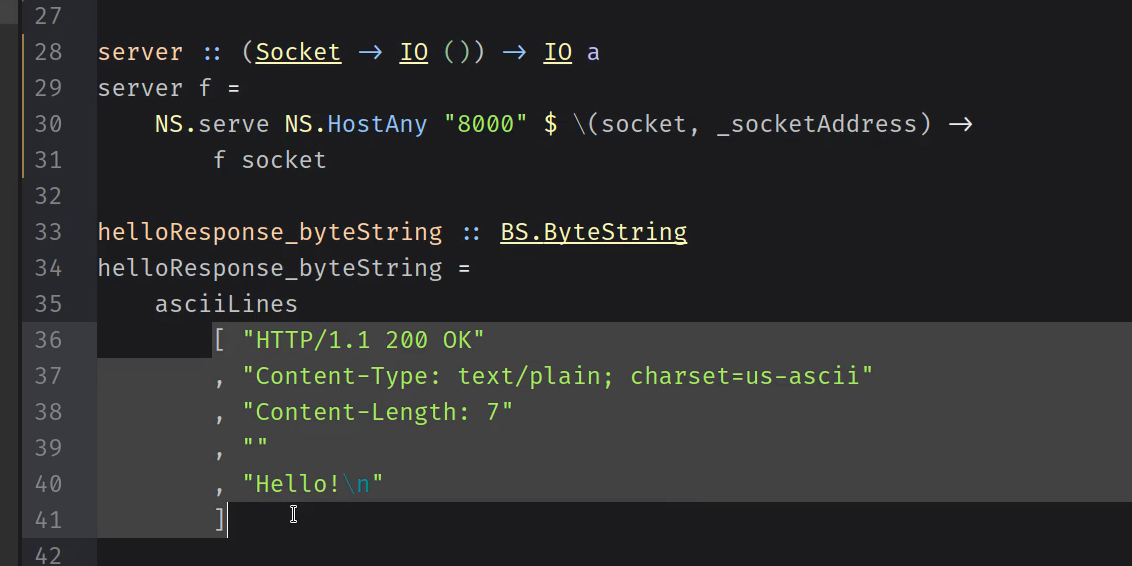
In the previous lesson, we started considering very basic web servers that only send one fixed response. We don’t want to write any more HTTP responses “by hand,” so here we look at what the format is, in general, so we can codify it in Haskell.

In Web Servers lesson 4, we write the function to convert an HTTP Response into a ByteString.

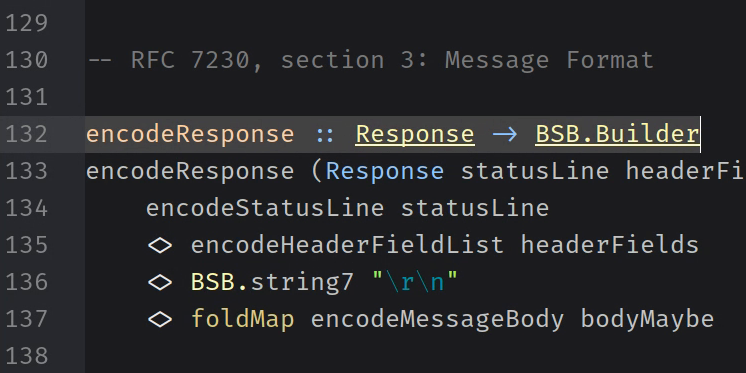
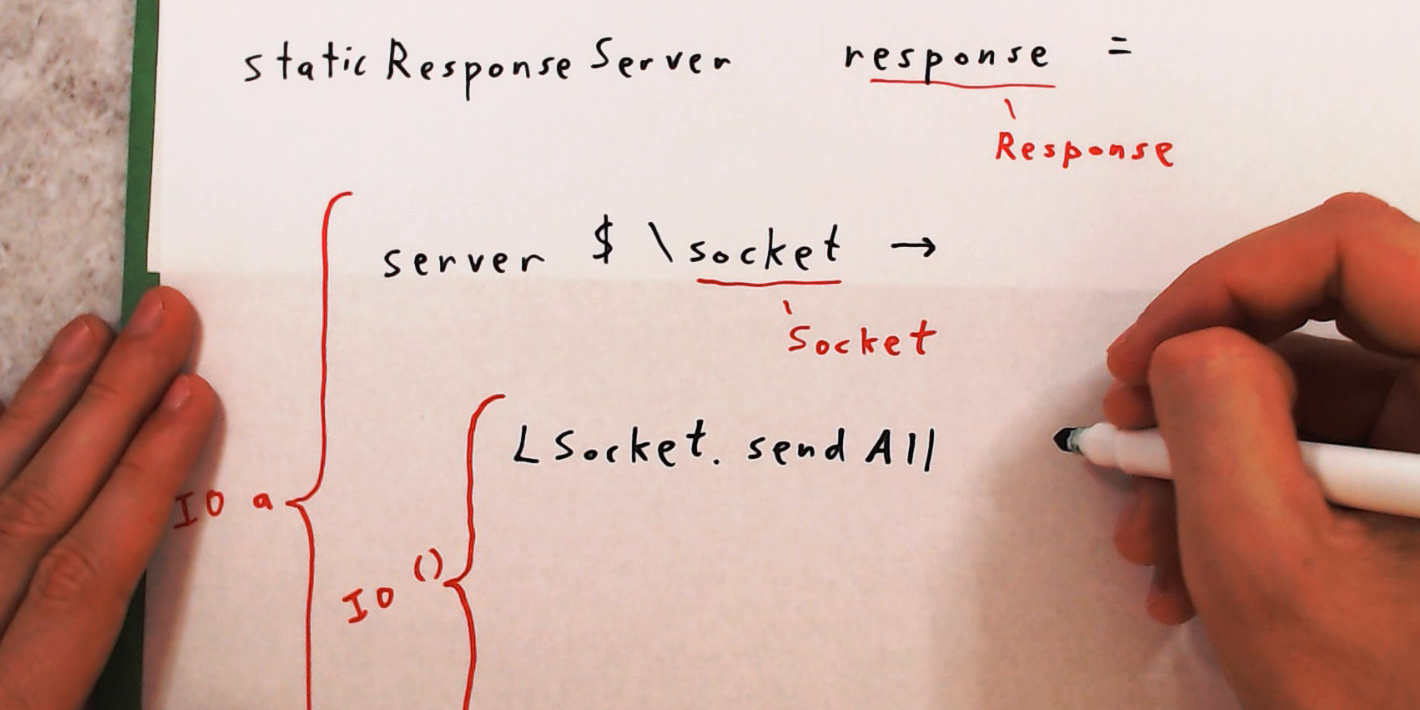
In Web Servers lesson 5, we use the encodeResponse function from the previous lesson to rewrite our HTTP server so that the response it sends is constructed from a value of the Response type.

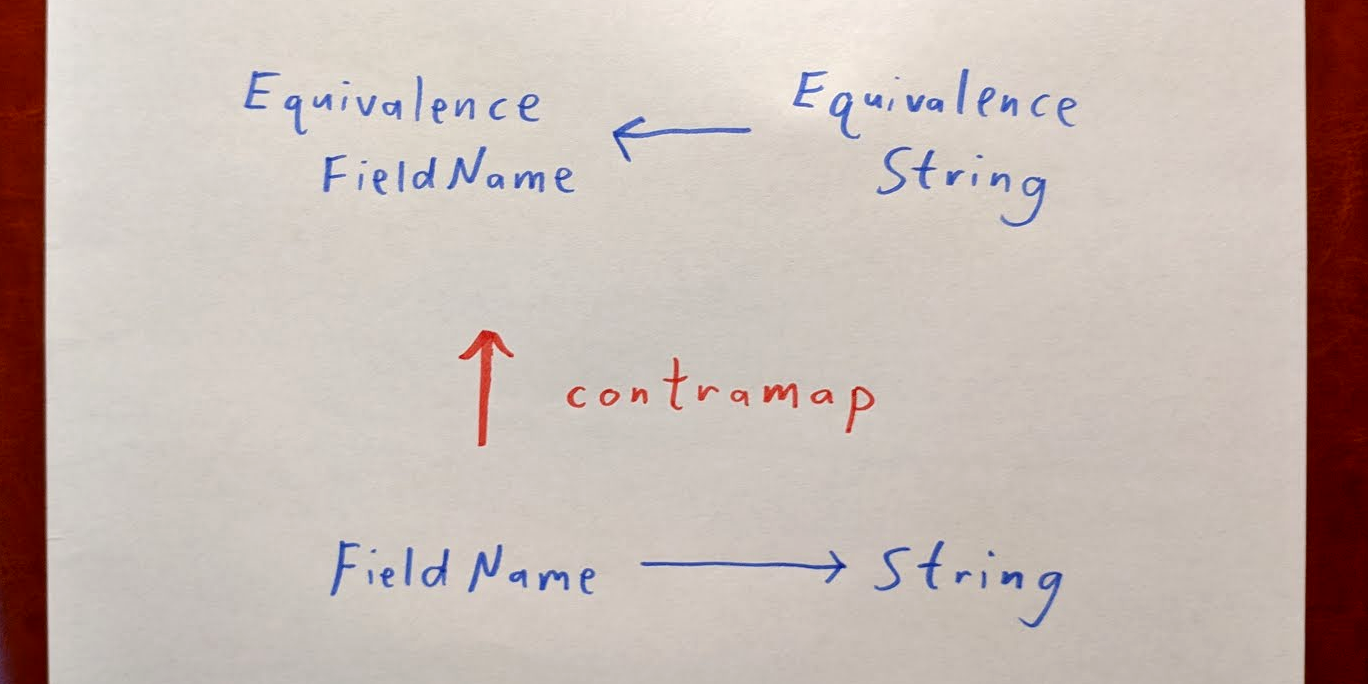
In this lesson, we write a function to manipulate lists of HTTP headers. Since field names are case-insensitive, we get to use ‘contramap’ to construct a case-insensitive Equivalence for them. We then use that to write a function that adds the appropriate “Content-Length” header to an HTTP response.

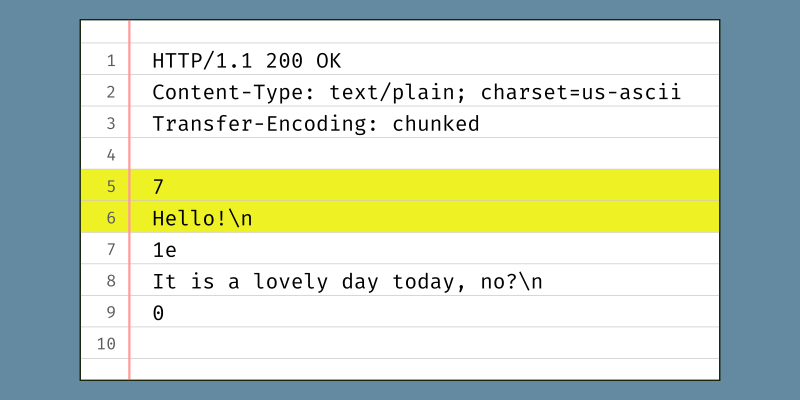
In the previous lesson, we wrote a function to set the Content-Length header on a response. This header tells the recipient how many bytes to expect in the message body. The Content-Length header field is one of two ways to let the client know when it’s time to stop waiting for more of the response to read. This lesson is about the second way: using the “Transfer-Encoding: chunked” header to specify that we are going to segment the message body in multiple smaller parts (“chunks”). The exercises in this lesson ask you to try things out using GHCi and curl; they do not require writing any code.

There’s one way you can clearly see the difference between strict and lazy data: Only lazy strings can be infinite. This lesson focuses on that fact and do an exercise to give you a little direct experience with it.

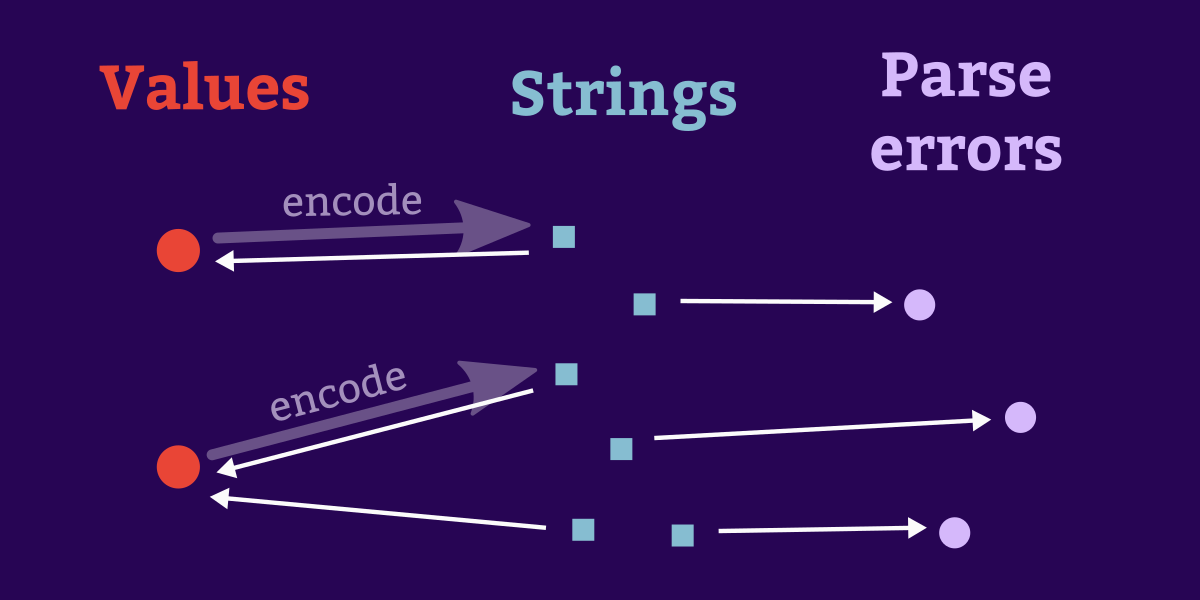
First we give background about parsing concepts, an introduction to some of the details of using the Attoparsec library, and discussion of the Alternative typeclass that so often comes up alongside parsers. Then we start writing the HTTP request parser, with a continued emphasis that transcribing the HTTP specification into Haskell is a methodical task for which careful reading is more important than cleverness.

A Python iterator is a sort of sequence that, unlike a list, computes each subsequent value only as it is needed rather than producing the entire list all at once. For example, from a range, we can produce an iterator of numbers. Here we construct an iterator xs that will produce three values: xs = iter(range(1, 4)). We can use the next function to demonstrate pulling values from the iterator one at a time.

There are several interrelated systems with “Nix” in their names. Nix is a language, a package manager, a build tool, a collection of packages, and an operating system.